发表于
字数统计: | 阅读时长 ≈

卷积神经网络基础

1.卷积运算

1.定义

2.动机

卷积运算改进机器学习系统的三个重要思想：

稀疏交互(saprse interactions)
又称稀疏权重(sparse weights)，这是因为核大小远小于输入大小。eg：当输入图像包含成千上万像素点，只采用几十个到上百个像素点的和来检测小而有意义的特征。
减少了存取需求，提高统计效率。

参数共享(parameter sharing)
是指，在一个模型中的多个函数中使用相同参数。卷积运算共享一个卷积核，保证我们只需学习一个参数集，而非在每一个位置学习同一个参数集。

等变表示(equivariant represetations)
如果一个函数满足输入改变，而输出也以同样方式改变则该函数是等变的。这在处理时间序列中事件延后，图像序列中对象的移动是非常有利的。
而一些其他的变换在卷积中并非必然。比如图像放缩和旋转变换，则需要其他机制处理。

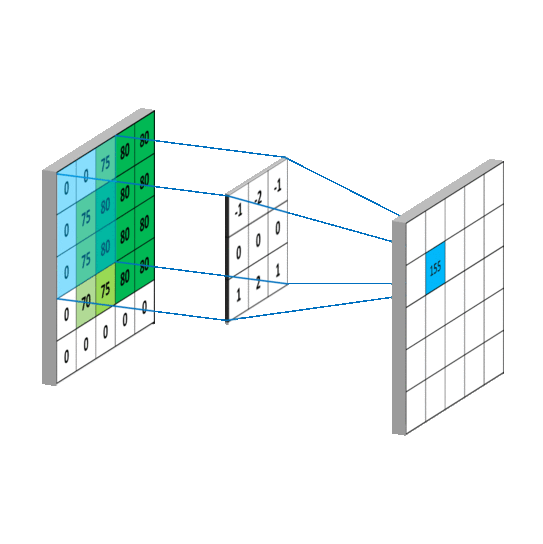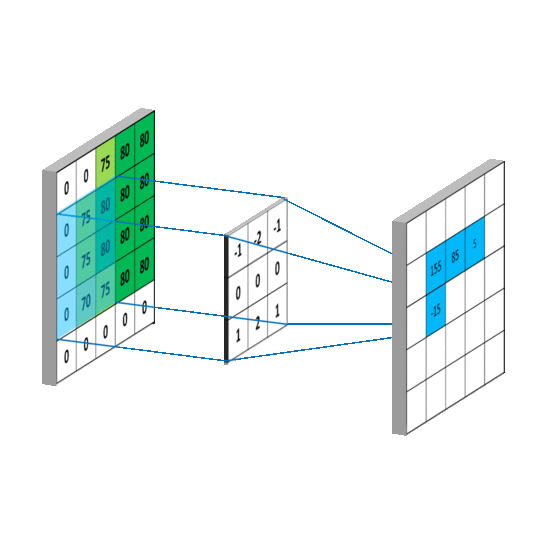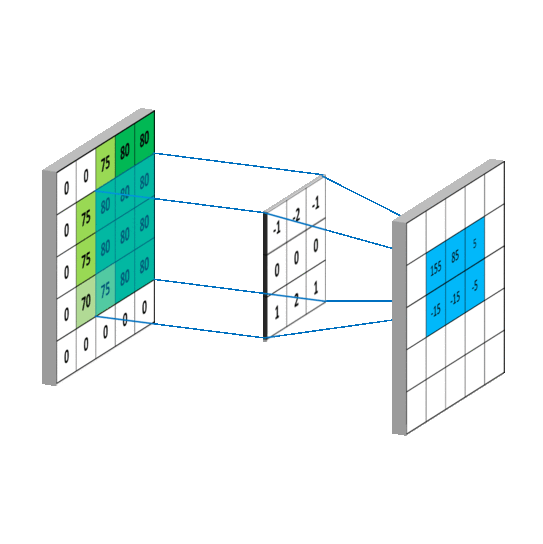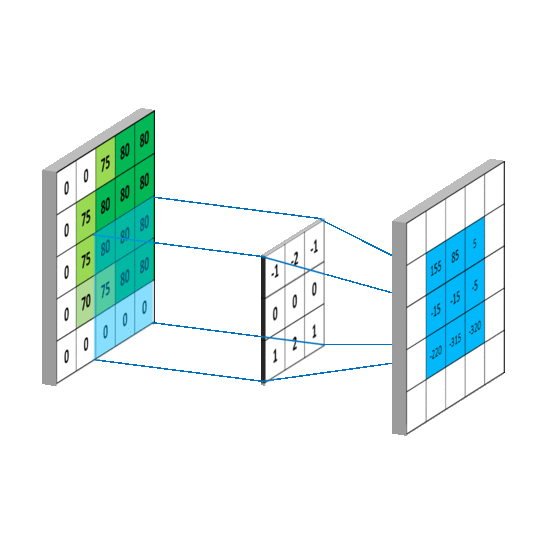
3.一维矩阵运算

在数学里我们知道f(-x)的图像是f(x)对y轴的反转

​ g(-m)就是把g(m)的序列反转，g(n-m)的意义是把g(-m)平移的n点：

卷积运算时可以交换顺序.

  • 代码实现

    1
    2
    3
    4
    5
    6
    import numpy as np
    x=np.array([1,2,3])
    h=np.array([2,3,1])
    import scipy.signal
    scipy.signal.convolve(x,h)
    print(scipy.signal.convolve(x,h))

4.二维矩阵运算

其中，矩阵A和B的尺寸分别为mana即mbnb

① 对矩阵A补零，

第一行之前和最后一行之后都补mb-1行，

第一列之前和最后一列之后都补nb-1列

（注意conv2不支持其他的边界补充选项，函数内部对输入总是补零）；

之所以都是-1是因为卷积核要在图像A上面移动,移动的时候需要满足两者至少有一列或者一行是重叠的.

再将卷积核旋转180度，之后有三种计算方式，分别是按照shape=full,shape=same,shape=valid进行计算(重叠部分进行矢量积运算)

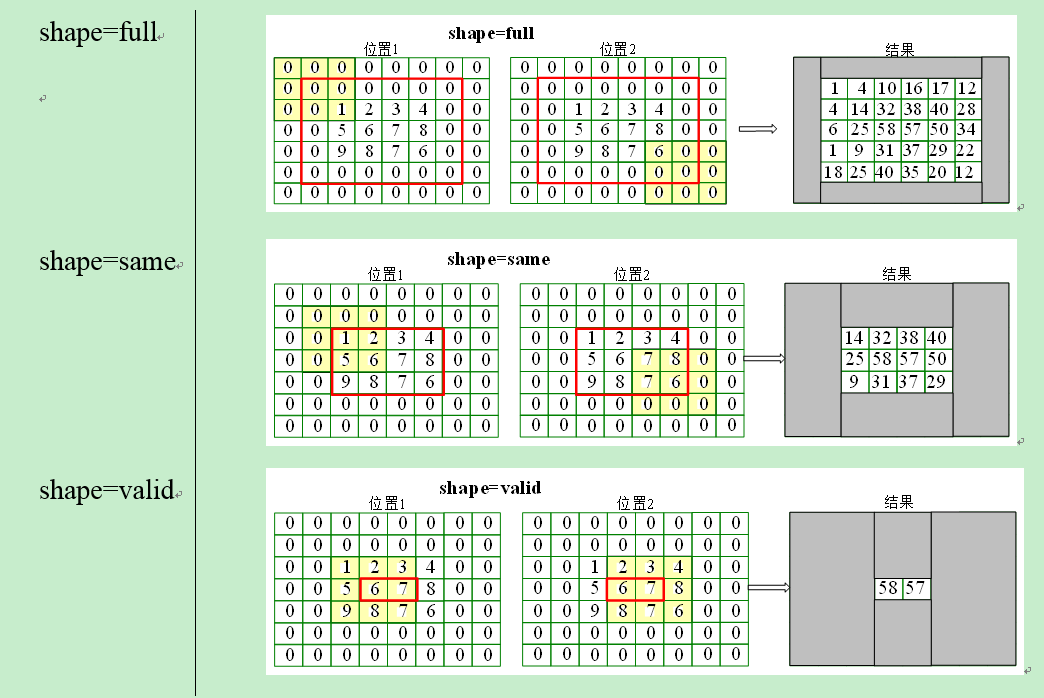
卷积层输入特征和输出特征尺寸和卷积核的关系

2.反卷积

我们把4×4的输入特征展成[16,1]的矩阵X ,那么Y = CX则是一个[4,1]的输出特征矩阵，把它重新排列2×2的输出特征就得到最终的结果，从上述分析可以看出卷积层的计算其实是可以转化成矩阵相乘的。值得注意的是，在一些深度学习网络的开源框架中并不是通过这种这个转换方法来计算卷积的，因为这个转换会存在很多无用的0乘操作，Caffe中具体实现卷积计算的方法可参考Implementing convolution as a matrix multiplication

​ 通过上述的分析，我们已经知道卷积层的前向操作可以表示为和矩阵C相乘，那么 我们很容易得到卷积层的反向传播就是和C的转置相乘。

这里提到的反卷积跟1维信号处理的反卷积计算是很不一样的，FCN作者称为backwards convolution，有人称Deconvolution layer is a very unfortunate name and should rather be called a transposed convolutional layer. 我们可以知道，在CNN中有con layer与pool layer，con layer进行对图像卷积提取特征，pool layer对图像缩小一半筛选重要特征，对于经典的图像识别CNN网络，如IMAGENET，最后输出结果是1X1X1000，1000是类别种类，1x1得到的是。FCN作者，或者后来对end to end研究的人员，就是对最终1x1的结果使用反卷积（事实上FCN作者最后的输出不是1X1，是图片大小的32分之一，但不影响反卷积的使用）。

这里图像的反卷积与图6的full卷积原理是一样的，使用了这一种反卷积手段使得图像可以变大，FCN作者使用的方法是这里所说反卷积的一种变体，这样就可以获得相应的像素值，图像可以实现end to end。

这里说另外一种反卷积做法，假设原图是3X3，首先使用上采样让图像变成7X7，可以看到图像多了很多空白的像素点。使用一个3X3的卷积核对图像进行滑动步长为1的valid卷积，得到一个5X5的图像，我们知道的是使用上采样扩大图片，使用反卷积填充图像内容，使得图像内容变得丰富，这也是CNN输出end to end结果的一种方法。韩国作者Hyeonwoo Noh使用VGG16层CNN网络后面加上对称的16层反卷积与上采样网络实现end to end 输出，其不同层上采样与反卷积变化效果如下:

3.图像卷积的再解释

基本方法（2种）：

方法1：full卷积,完整的卷积使得原来的定义变大

方法2：记录pooling index,然后扩大空间

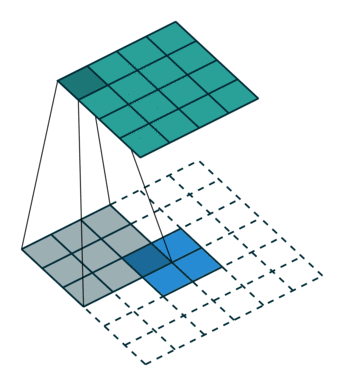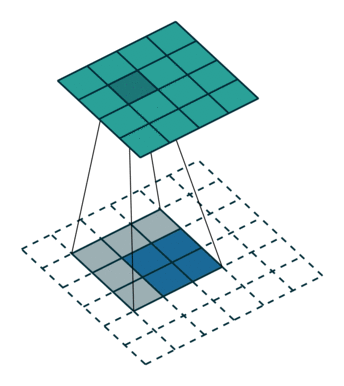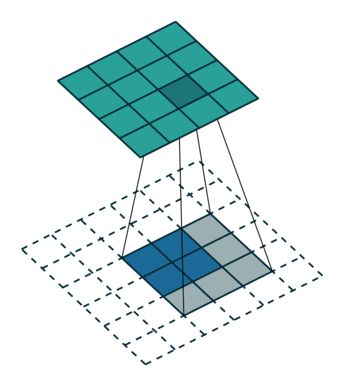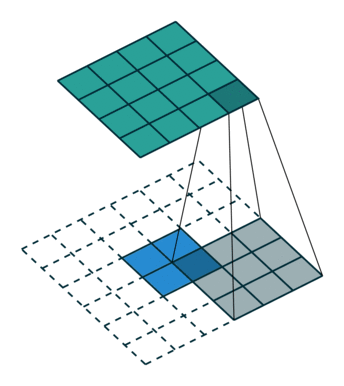
图像的反卷积过程如下：

  1. 输入图片每个像素进行一次full卷积，根据full卷积大小计算可以知道每个像素的卷积后大小为 1+4-1=4， 即4x4大小的特征图，输入有4个像素所以4个4x4的特征图
  2. 将4个特征图进行步长为3的fusion（即相加）； 例如红色的特征图仍然是在原来输入位置（左上角），绿色还是在原来的位置（右上角），步长为3是指每隔3个像素进行fusion，重叠部分进行相加，即输出的第1行第4列是由红色特阵图的第一行第四列与绿色特征图的第一行第一列相加得到，其他如此类推。

2.池化运算

池化层往往在卷积层后面，通过池化来降低卷积层输出的特征向量，同时改善结果（不易出现过拟合）。图像具有一种“静态性”的属性，这也就意味着在一个图像区域有用的特征极有可能在另一个区域同样适用。因此，为了描述大的图像，一个很自然的想法就是对不同位置的特征进行聚合统计，例如，人们可以计算图像一个区域上的某个特定特征的平均值 (或最大值)来代表这个区域的特征

1.Max pooling池化操作

利用CNN卷积神经网络进行训练时，进行完卷积运算，还需要接着进行Max pooling池化操作，目的是在尽量不丢失图像特征前期下，对图像进行downsampling。

整个图片被不重叠的分割成若干个同样大小的小块（pooling size）。每个小块内只取最大的数字，再舍弃其他节点后，保持原有的平面结构得出 output。

是利用平移不变性

如下面，先进行卷积操作，再进行池化操作：

2.一般池化

池化窗口和窗口移动的距离大小是相等的

3.重叠池化

重叠池化正如其名字所说的，相邻池化窗口之间会有重叠区域

4.空金字塔池化

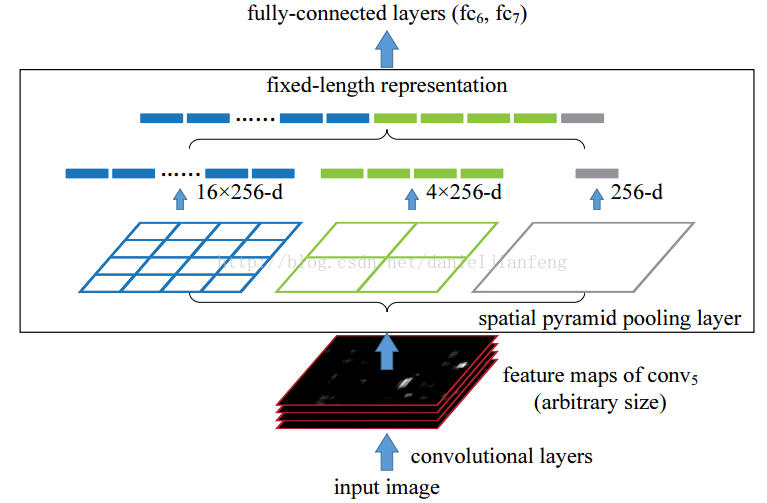
先让图像进行卷积操作，然后转化成维度相同的特征输入到全连接层，这个可以把CNN扩展到任意大小的图像。

空间金字塔池化的思想来自于Spatial Pyramid Model，它一个pooling变成了多个scale的pooling。用不同大小池化窗口作用于卷积特征，我们可以得到1X1,2X2,4X4的池化结果，由于conv5中共有256个过滤器，所以得到1个256维的特征，4个256个特征，以及16个256维的特征，然后把这21个256维特征链接起来输入全连接层，通过这种方式把不同大小的图像转化成相同维度的特征。

3.Text-CNN原理及文本分类模型

1.原理

具体过程如下

  • Embedding：第一层是图中最左边的7乘5的句子矩阵，每行是词向量，维度=5，这个可以类比为图像中的原始像素点。
  • Convolution：然后经过 kernel_sizes=(2,3,4) 的一维卷积层，每个kernel_size 有两个输出 channel。
  • MaxPolling：第三层是一个1-max pooling层，这样不同长度句子经过pooling层之后都能变成定长的表示。

  • FullConnection and Softmax：最后接一层全连接的 softmax 层，输出每个类别的概率。

    文本是一维数据，因此在TextCNN卷积用的是一维卷积（在word-level上是一维卷积；虽然文本经过词向量表达后是二维数据，但是在embedding-level上的二维卷积没有意义）。一维卷积带来的问题是需要通过设计不同 kernel_size 的 filter 获取不同宽度的视野。

CNN的卷积和池化的过程就是一个抽取特征的过程（摘自CNN原理文本分类)

2004年Yoon Kim 在 “Convolutional Neural Networks for Sentence Classification” 一文中提出（虽然第一个用的并不是他，但是在这篇文章中提出了4种Model Variations，并有详细的调参）：

论文使用的模型主要包括五层，第一层是embedding layer,第二层是convolutional layer,第三层是max-pooling layer,第四层是fully connected layer，最后一层是softmax layer.

  • 为了使其可以进行卷积，首先需要将其转化为二维矩阵表示，通常使用word2vec、glove等word embedding实现。d=5表示每个词转化为5维的向量，矩阵的形状是[sentence_matrix × 5]，即[7 × 5]。

  • 在处理图像数据时，CNN使用的卷积核的宽度和高度的一样的，但是在text-CNN中，卷积核的宽度是与词向量的维度一致。这是因为我们输入的每一行向量代表一个词，在抽取特征的过程中，词做为文本的最小粒度，如果我们使用卷积核的宽度小于词向量的维度就已经不是以词作为最小粒度了。而高度和CNN一样，可以自行设置（通常取值2,3,4,5）。由于我们的输入是一个句子，句子中相邻的词之间关联性很高，因此，当我们用卷积核进行卷积时，不仅考虑了词义而且考虑了词序及其上下文。（类似于skip-gram和CBOW模型的思想）。
    详细讲解卷积的过程：卷积层输入的是一个表示句子的矩阵，维度为n*d，即每句话共有n个词，每个词有一个d维的词向量表示。假设Xi:i+j表示Xi到Xi+j个词，使用一个宽度为d，高度为h的卷积核W与Xi:i+h-1(h个词)进行卷积操作后再使用激活函数激活得到相应的特征ci，则卷积操作可以表示为：（使用点乘来表示卷积操作）

  • 在文本分类中常用的步长是1,更大的补偿会使得向神经网络靠近

  • 窄卷积 vs 宽卷积

    在矩阵的中部使用卷积核滤波没有问题，在矩阵的边缘，如对于左侧和顶部没有相邻元素的元素，该如何滤波呢？解决的办法是采用补零法（zero-padding）。所有落在矩阵范围之外的元素值都默认为0。这样就可以对输入矩阵的每一个元素做滤波了，输出一个同样大小或是更大的矩阵。补零法又被称为是宽卷积，不使用补零的方法则被称为窄卷积。

  • 池化:Max-Pooling之后，还需要将每个值给拼接起来。得到池化层最终的特征向量。在池化层到全连接层之前可以加上dropout防止过拟合。

​ 文本中pooling方法的优缺点:

  • Max Pooling over time

    这个操作可以保证特征的位置与旋转不变性，对于图像处理来说这种位置与旋转不变性是很好的特性，但是对于NLP来说，这个特性其实并不一定是好事，因为在很多NLP的应用场合，特征的出现位置信息是很重要的，比如主语出现位置一般在句子头，宾语一般出现在句子尾等等，这些位置信息其实有时候对于分类任务来说还是很重要的，但是Max Pooling 基本把这些信息抛掉了。其次，MaxPooling能减少模型参数数量，有利于减少模型过拟合问题。再者，对于NLP任务来说，Max Pooling可以把变长的输入X整理成固定长度的输入。
    但是，CNN模型采取MaxPooling Over Time也有一些值得注意的缺点：首先就如上所述，特征的位置信息在这一步骤完全丢失。在卷积层其实是保留了特征的位置信息的，但是通过取唯一的最大值，现在在Pooling层只知道这个最大值是多少，但是其出现位置信息并没有保留；另外一个明显的缺点是：有时候有些强特征会出现多次，比如我们常见的TF.IDF公式，TF就是指某个特征出现的次数，出现次数越多说明这个特征越强，但是因为Max Pooling只保留一个最大值，所以即使某个特征出现多次，现在也只能看到一次，就是说同一特征的强度信息丢失了。这是Max Pooling Over Time典型的两个缺点。

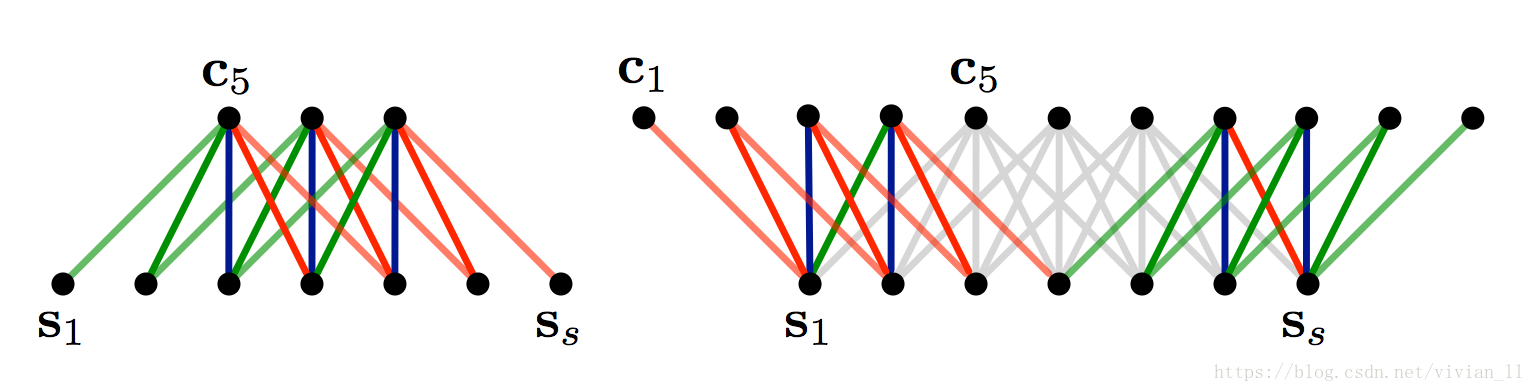
  • K-Max pooling

    取所有特征值中得分在Top –K的值，并保留这些特征值原始的先后顺序（下图是2-max Pooling的示意图），就是说通过多保留一些特征信息供后续阶段使用

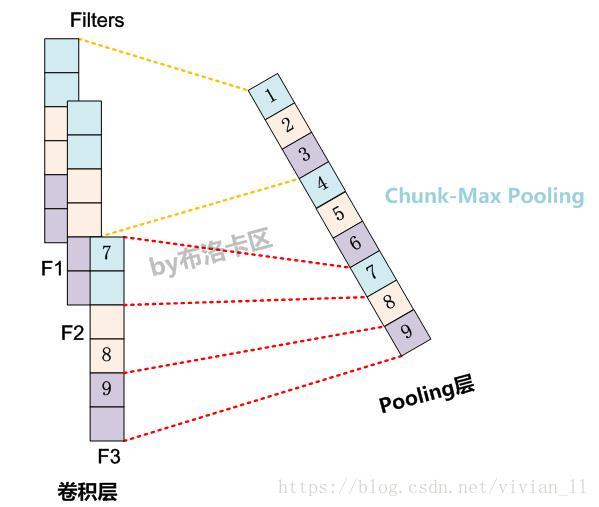
  • Chunk-Max pooling

  • Chunk-MaxPooling的思想是：把某个Filter对应的Convolution层的所有特征向量进行分段，切割成若干段后，在每个分段里面各自取得一个最大特征值，比如将某个Filter的特征向量切成3个Chunk，那么就在每个Chunk里面取一个最大值，于是获得3个特征值。（如下图所示，不同颜色代表不同分段）

  • 全连接层跟其他模型一样，假设有两层全连接层，第一层可以加上relu作为激活函数，对于多分类来说，第二层则使用softmax激活函数得到属于每个类的概率，并选择categorical_crossentropy 作为激活函数。如果处理的数据集为二分类问题，如情感分析的正负面时，第二层也可以使用sigmoid作为激活函数，然后损失函数使用对数损失函数binary_crossentropy。

    *将不同的词向量表征看成是不同的通道：

    • CNN-rand: 随机初始化每个单词的词向量通过后续的训练去调整。
    • CNN-static: 使用预先训练好的词向量，如word2vec训练出来的词向量，在训练过程中不再调整该词向量。
    • CNN-non-static: 使用预先训练好的词向量，并在训练过程进一步进行调整。
    • CNN-multichannel: 将static与non-static作为两通道的词向量。

发表于
字数统计: | 阅读时长 ≈ 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import tensorflow as tf
import pandas as pd
import numpy as np
#生产数据集
D=2#X的特征个数
K=300
C=2#输出Y的几类
X=(np.random((K,D))*10)-5
Y_c=[int(x0*x0+x1*x1<9) for (x0,x1) in X]
Y=pd.get_dummies(Y_c).values#one-hot

#构建网络模型
def get_weight(shape,reg):
    w=tf.Variable(tf.random_normal(shape),dtype=tf.float32)
    #如果进行正则化将损失值加入到loss中
    tf.add_to_collection('losses',tf.contrib.layers.l2_regularizer(reg)(w))
    return w

def get_bais(shape):
    return tf.Variable(tf.constant(0.0,shape=shape,dtypeype=tf.float32))
#输入输出占位
x=tf.placeholder(dtype=tf.float32,shape=(None,D))
y=tf.placeholder(dtype=float32,shape=(None,C))#输入数据的量不确定，使用None占位
h=100
#构建网络
w1=get_weight([D,h],1e-3)
b1=get_bais([1,h])
#隐藏层使用激活函数relu
y1=tf.nn.relu(tf.matmul(x,w1)+b1)

w2=get_weight([h,C],1e-3)
b2=get_bias([1,C])
y_=tf.matmul(y1,w2)+b2
 
#参数设置
STEPS=2000
BATCH_SIZE=256
#学习率
learning_rate=1e-0

#数据损失
data_loss=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(labels = y,logits =y_))#交叉熵
#正则损失
reg_loss=tf.add_n(tf.get_collection("losses"))
total_loss=reg_loss+data_loss

#定义训练方式-梯度下降
train_function=tf.train.GradientDescentOptimizer(learning_rate).minimize(total_loss)

#开始训练
with tf.Session() as sess:
    init_op=tf.global_variables_initializervar()
    sess.run(init_op)
    fpr i in range(STEPS):
        start=(i*BATCH_SIZE)%k
        end=start+BATCH_SIZE
        sess.run(train_function,feed_dict={x:X[start:end],y:Y[start:end]})
        if i%100==0:
#             # 计算当前数据损失值
            loss_v = sess.run(data_loss,feed_dict={x:X,y:Y})
            print("this is %dth step,the loss is %f"%(i,loss_v))

发表于
字数统计: | 阅读时长 ≈

简单神经网络（2）

1.词袋模型(bow : 离散、高维、稀疏)

在自然语言处理和文本分析的问题中，词袋（Bag of Words, BOW）和词向量（Word Embedding）是两种最常用的模型。更准确地说，词向量只能表征单个词，如果要表示文本，需要做一些额外的处理。所谓BOW，就是将文本/Query看作是一系列词的集合。

  • 离散：无法衡量词向量之间的关系, 比如酒店、宾馆、旅社 三者都只在某一个固定的位置为 1 ，所以找不到三者的关系，各种度量(与或非、距离)都不合适，即太稀疏，很难捕捉到文本的含义。

  • 高维：词表维度随着语料库增长膨胀，n-gram 序列随语料库膨胀更快。

  • 数据稀疏： 数据都没有特征多，数据有 100 条，特征有 1000 个

举个例子：
文本1：苏宁易购/是/国内/著名/的/B2C/电商/之一
这是一个短文本。“/”作为词与词之间的分割。从中我们可以看到这个文本包含“苏宁易购”，“B2C”，“电商”等词。换句话说，该文本的的词袋由“苏宁易购”，“电商”等词构成。就像这样：

但计算机不认识字，只认识数字，那在计算机中怎么表示词袋模型呢？其实很简单，给每个词一个位置/索引就可以了。例如，我们令“苏宁易购”的索引为0，“电商”的索引为1，其他以此类推。则该文本的词袋就变成了：

词袋是在词集的基础上增加了频率的维度，词集只关注有和没有，词袋还要关注有几个。

假设我们要对一篇文章进行特征化，最常见的方式就是词袋。

假如现在有1000篇新闻文档，把这些文档拆成一个个的字，去重后得到3000个字，然后把这3000个字作为字典，进行文本表示的模型，叫做词袋模型。这种模型的特点是字典中的字没有特定的顺序，句子的总体结构也被舍弃了.

  • 2.分布式表示(连续，稠密，低维)

分布式（distributed）描述的是把
信息分布式地存储在向量的各个维度中，与之相对的是局部表示（local
representation），如词的独热表示（one-hot representation），在高维向量中
只有一个维度描述了词的语义。一般来说，通过矩阵降维或神经网络降维
可以将语义分散存储到向量的各个维度中，因此，这类方法得到的低维向 量一般都可以称作分布式表示。

2.word2vec代码实现

3.bow2vec + TFIDF模型

主要内容为：
拆分句子为单词颗粒，记号化；
生成词典；
生成稀疏文档矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
documents = ["Human machine interface for lab abc computer applications",
             "A survey of user opinion of computer system response time",
             "The EPS user interface management system",
             "System and human system engineering testing of EPS",              
             "Relation of user perceived response time to error measurement",
             "The generation of random binary unordered trees",
             "The intersection graph of paths in trees",
             "Graph minors IV Widths of trees and well quasi ordering",
             "Graph minors A survey"]

# 分词并根据词频剔除
# remove common words and tokenize
stoplist = set('for a of the and to in'.split())
texts = [[word for word in document.lower().split() if word not in stoplist]
         for document in documents]
         
         #分词并根据词频剔除
#将句子划分为词
stoplist=set('for a of the end to in'.split())
texts=[[word for word in document.lower().split() if word not in stoplist] for document in documents]
print(texts)

#生成词典
from gensim import corpora
import os
dictionary=corpora.Dictionary(texts)
dictionary.save(os.path.join('C:/Users/wuxun/Desktop/','deerwester.dict'))#存储词典#路径拼接函数
print(dictionary)
print(dictionary.token2id)
tfidf
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#生成词袋
new_doc="Human computer interaction Human"
new_vec=dictionary.doc2bow(new_doc.lower().split())
print(new_vec)
# the word "interaction" does not appear in the dictionary and is ignored
    # [(0, 1), (1, 1)] ，词典（dictionary）中第0个词，出现的频数为1（当前句子），
    # 第1个词，出现的频数为1
#多句bow生成
[dictionary.doc2bow(text) for text in texts]
#print(texts)

from gensim import corpora,models,similarities
corpus = [[(0, 1.0), (1, 1.0), (2, 1.0)],
          [(2, 1.0), (3, 1.0), (4, 1.0), (5, 1.0), (6, 1.0), (8, 1.0)],
          [(1, 1.0), (3, 1.0), (4, 1.0), (7, 1.0)],
          [(0, 1.0), (4, 2.0), (7, 1.0)],
          [(3, 1.0), (5, 1.0), (6, 1.0)],
          [(9, 1.0)],
          [(9, 1.0), (10, 1.0)],
          [(9, 1.0), (10, 1.0), (11, 1.0)],
          [(8, 1.0), (10, 1.0), (11, 1.0)]]
tfidf=models.TfidfModel(corpus)

#词袋模型，实践
vec=[(0,1),(4,1),(9,1)]
print(tfidf[vec])
#查找vec中，0,4,9号三个词的TFIDF值。同时进行转化，把之前的文档矩阵中的词频变成了TFIDF值。
#利用tfidf求相似：

index=similarities.SparseMatrixSimilarity(tfidf[corpus],num_features=12)
vec=[(0,1),(4,1),(9,1)]
sims=index[tfidf[vec]]
#对corpus中的九个文档进行文档级别索引，vec是新文档的词袋,sim就是该vec向量对corpus中九个文档的相似性
print(list(enumerate(sims)))

发表于
字数统计: | 阅读时长 ≈

简单神经网络

1.文本表示

(1).one-hot

one-hot即独立热词，词语被表示成一个维度为词表大小的向量，这个向量中只有一个维度是1其他位置都是0.假如词表中只有四个个词“奥巴马”、“特朗普”、“宣誓”、“就职”，那么他们将被表示为：

one-hot表示的优点是简单易用，但是有着致命的缺点：

  • 如果一个词表有十万个单词，那么就需要十万维的向量来表示每一个单词，而每个向量只有一位是1，在储存上造成大量浪费，在深度学习场景中容易受到维度灾难的困扰。
  • 奥巴马和特朗普都是美国总统，而one-hot表示出的两个向量是正交向量，也就是他们之间毫无关系，这显然是丢失了相关语义信息。
    因此我们需要更好的表示方法。

实例例举：

word2vec

word2vec就是将词表征为实数值向量的一种高效的算法模型，其利用深度学习的思想，可以通过训练，把对文本内容的处理简化为 K 维向量空间中的向量运算，而向量空间上的相似度可以用来表示文本语义上的相似。当我们在说word2vec算法或模型的时候，其实指的是其背后用于计算word vector的CBoW模型和Skip-gram模型。很多人以为word2vec指的是一个算法或模型，这也是一种谬误。

  • 引子：Distributed representation词向量表示

    低维实数向量。向量的距离可以用最传统的欧氏距离来衡量，也可以用 cos 夹角来衡量。它的思路是通过训练，将每个词都映射到一个较短的词向量上来。所有的这些词向量就构成了向量空间，进而可以用普通的统计学的方法来研究词与词之间的关系。这个较短的词向量维度是多大呢？这个一般需要我们在训练时自己来指定。

  • Word2vec 使用的词向量不是我们上述提到的One-hot Representation那种词向量，而是 Distributed representation 的词向量表示方式。其基本思想是 通过训练将每个词映射成 K 维实数向量（K 一般为模型中的超参数），通过词之间的距离（比如 cosine 相似度、欧氏距离等）来判断它们之间的语义相似度.其采用一个 三层的神经网络 ，输入层-隐层-输出层。有个核心的技术是 根据词频用Huffman编码 ，使得所有词频相似的词隐藏层激活的内容基本一致，出现频率越高的词语，他们激活的隐藏层数目越少，这样有效的降低了计算的复杂度。而Word2vec大受欢迎的一个原因正是其高效性。这个三层神经网络本身是 对语言模型进行建模 ，但也同时 获得一种单词在向量空间上的表示 ，而这个副作用才是Word2vec的真正目标。

  • 输入是one-hot,，Hidden Layer没有激活函数，也就是线性的单元。Output Layer维度跟Input Layer的维度一样，用的是Softmax回归。当这个模型训练好以后，我们并不会用这个训练好的模型处理新的任务，我们真正需要的是这个模型通过训练数据所学得的参数，例如隐层的权重矩阵。

Word2Vec实际上是两种不同的方法：Continuous Bag of Words (CBOW) 和 Skip-gram。CBOW的目标是根据上下文来预测当前词语的概率。Skip-gram刚好相反：根据当前词语来预测上下文的概率（如下图所示）。这两种方法都利用人工神经网络作为它们的分类算法。起初，每个单词都是一个随机 N 维向量。经过训练之后，该算法利用 CBOW 或者 Skip-gram 的方法获得了每个单词的最优向量。

　取一个适当大小的窗口当做语境，输入层读入窗口内的词，将它们的向量（K维，初始随机）加和在一起，形成隐藏层K个节点。输出层是一个巨大的二叉 树，叶节点代表语料里所有的词（语料含有V个独立的词，则二叉树有|V|个叶节点）。而这整颗二叉树构建的算法就是Huffman树。这样，对于叶节点的 每一个词，就会有一个全局唯一的编码，形如”010011”，不妨记左子树为1，右子树为0。接下来，隐层的每一个节点都会跟二叉树的内节点有连边，于是 对于二叉树的每一个内节点都会有K条连边，每条边上也会有权值。

对于语料库中的某个词w_t，对应着二叉树的某个叶子节点，因此它必然有一个二进制编码，如”010011”。在训练阶段，当给定上下文，要预测后 面的词w_t的时候，我们就从二叉树的根节点开始遍历，这里的目标就是预测这个词的二进制编号的每一位。即对于给定的上下文，我们的目标是使得预测词的二 进制编码概率最大。形象地说，我们希望在根节点，词向量和与根节点相连经过 logistic 计算得到 bit=1 的概率尽量接近 0，在第二层，希望其 bit=1 的概率尽量接近1，这么一直下去，我们把一路上计算得到的概率相乘，即得到目标词w_t在当前网络下的概率P(w_t)，那么对于当前这个 sample的残差就是1-P(w_t)，于是就可以使用梯度下降法训练这个网络得到所有的参数值了。显而易见，按照目标词的二进制编码计算到最后的概率 值就是归一化的。

　　最先优化使用的数据结构是用霍夫曼树来代替隐藏层和输出层的神经元，霍夫曼树的叶子节点起到输出层神经元的作用，叶子节点的个数即为词汇表的小大,word2vec使用霍夫曼树来代替传统的DNN算法（因为DNN算法处理过程非常耗时）。 而内部节点则起到隐藏层神经元的作用。其实借助了分类问题中，使用一连串二分类近似多分类的思想。例如我们是把所有的词都作为输出，那么“桔 子”、“汽车”都是混在一起。给定w_t的上下文，先让模型判断w_t是不是名词，再判断是不是食物名，再判断是不是水果，再判断是不是“桔子”。

　　但是在训练过程中，模型会赋予这些抽象的中间结点一个合适的向量，这个向量代表了它对应的所有子结点。因为真正的单词公用了这些抽象结点的向量，所 以Hierarchical Softmax方法和原始问题并不是等价的，但是这种近似并不会显著带来性能上的损失同时又使得模型的求解规模显著上升。

　　没有使用这种二叉树，而是直接从隐层直接计算每一个输出的概率——即传统的Softmax，就需要对|V|中的每一个词都算一遍，这个过程时间复杂 度是O(|V|)的。而使用了二叉树（如Word2vec中的Huffman树），其时间复杂度就降到了O(log2(|V|))，速度大大地加快了。

　　现在这些词向量已经捕捉到上下文的信息。我们可以利用基本代数公式来发现单词之间的关系（比如，“国王”-“男人”+“女人”=“王后”）。这些词向量可 以代替词袋用来预测未知数据的情感状况。该模型的优点在于不仅考虑了语境信息还压缩了数据规模（通常情况下，词汇量规模大约在300个单词左右而不是之前 模型的100000个单词）。因为神经网络可以替我们提取出这些特征的信息，所以我们仅需要做很少的手动工作。但是由于文本的长度各异，我们可能需要利用 所有词向量的平均值作为分类算法的输入值，从而对整个文本文档进行分类处理。

注：以下内容转载自网络

. 基于Hierarchical Softmax的模型概述

　　　　我们先回顾下传统的神经网络词向量语言模型，里面一般有三层，输入层（词向量），隐藏层和输出层（softmax层）。里面最大的问题在于从隐藏层到输出的softmax层的计算量很大，因为要计算所有词的softmax概率，再去找概率最大的值。这个模型如下图所示。其中VV 是词汇表的大小，

　　　　word2vec对这个模型做了改进，首先，对于从输入层到隐藏层的映射，没有采取神经网络的线性变换加激活函数的方法，而是采用简单的对所有输入词向量求和并取平均的方法。比如输入的是三个4维词向量：(1,2,3,4),(9,6,11,8),(5,10,7,12)(1,2,3,4),(9,6,11,8),(5,10,7,12) ,那么我们word2vec映射后的词向量就是(5,6,7,8)(5,6,7,8) 。由于这里是从多个词向量变成了一个词向量。

　　　　第二个改进就是从隐藏层到输出的softmax层这里的计算量个改进。为了避免要计算所有词的softmax概率，word2vec采样了霍夫曼树来代替从隐藏层到输出softmax层的映射。我们在上一节已经介绍了霍夫曼树的原理。如何映射呢？这里就是理解word2vec的关键所在了。

　　　　由于我们把之前所有都要计算的从输出softmax层的概率计算变成了一颗二叉霍夫曼树，那么我们的softmax概率计算只需要沿着树形结构进行就可以了。如下图所示，我们可以沿着霍夫曼树从根节点一直走到我们的叶子节点的词w2w2 。

　　　　和之前的神经网络语言模型相比，我们的霍夫曼树的所有内部节点就类似之前神经网络隐藏层的神经元,其中，根节点的词向量对应我们的投影后的词向量，而所有叶子节点就类似于之前神经网络softmax输出层的神经元，叶子节点的个数就是词汇表的大小。在霍夫曼树中，隐藏层到输出层的softmax映射不是一下子完成的，而是沿着霍夫曼树一步步完成的，因此这种softmax取名为”Hierarchical Softmax”。

　　　　如何“沿着霍夫曼树一步步完成”呢？在word2vec中，我们采用了二元逻辑回归的方法，即规定沿着左子树走，那么就是负类(霍夫曼树编码1)，沿着右子树走，那么就是正类(霍夫曼树编码0)。判别正类和负类的方法是使用sigmoid函数，即：

P(+)=σ(xTw**θ)=11+e−xTw**θP(+)=σ(xwTθ)=11+e−xwTθ

　　　　其中x**wxw 是当前内部节点的词向量，而θθ 则是我们需要从训练样本求出的逻辑回归的模型参数。

　　　　使用霍夫曼树有什么好处呢？首先，由于是二叉树，之前计算量为VV ,现在变成了log2Vlog2V 。第二，由于使用霍夫曼树是高频的词靠近树根，这样高频词需要更少的时间会被找到，这符合我们的贪心优化思想。

　　　　容易理解，被划分为左子树而成为负类的概率为P(−)=1−P(+)P(−)=1−P(+) 。在某一个内部节点，要判断是沿左子树还是右子树走的标准就是看P(−),P(+)P(−),P(+) 谁的概率值大。而控制P(−),P(+)P(−),P(+) 谁的概率值大的因素一个是当前节点的词向量，另一个是当前节点的模型参数θθ 。

　　　　对于上图中的w2w2 ，如果它是一个训练样本的输出，那么我们期望对于里面的隐藏节点n(w2,1)n(w2,1) 的P(−)P(−) 概率大，n(w2,2)n(w2,2) 的P(−)P(−) 概率大，n(w2,3)n(w2,3) 的P(+)P(+) 概率大。

　　　　回到基于Hierarchical Softmax的word2vec本身，我们的目标就是找到合适的所有节点的词向量和所有内部节点θθ , 使训练样本达到最大似然。那么如何达到最大似然呢？

2. 基于Hierarchical Softmax的模型梯度计算

　　　我们使用最大似然法来寻找所有节点的词向量和所有内部节点θθ 。先拿上面的w2w2 例子来看，我们期望最大化下面的似然函数：

∏i=13P(n(w**i),i)=(1−11+e−xTw**θ1)(1−11+e−xTw**θ2)11+e−xTw**θ3∏i=13P(n(wi),i)=(1−11+e−xwTθ1)(1−11+e−xwTθ2)11+e−xwTθ3

　　　　对于所有的训练样本，我们期望最大化所有样本的似然函数乘积。

　　　　为了便于我们后面一般化的描述，我们定义输入的词为ww ,其从输入层词向量求和平均后的霍夫曼树根节点词向量为x**wxw , 从根节点到ww 所在的叶子节点，包含的节点总数为l**wlw , ww 在霍夫曼树中从根节点开始，经过的第ii 个节点表示为pwipiw ,对应的霍夫曼编码为dwi∈{0,1}diw∈{0,1} ,其中i=2,3,…l**wi=2,3,…lw 。而该节点对应的模型参数表示为θwiθiw , 其中i=1,2,…l**w−1i=1,2,…lw−1 ，没有i=l**wi=lw 是因为模型参数仅仅针对于霍夫曼树的内部节点。

　　　　定义ww 经过的霍夫曼树某一个节点j的逻辑回归概率为P(dwj|x**w,θwj−1)P(djw|xw,θj−1w) ，其表达式为：

P(dwj|x**w,θwj−1)={σ(xTwθw**j−1)1−σ(xTwθw**j−1)dwj=0dwj=1P(djw|xw,θj−1w)={σ(xwTθj−1w)djw=01−σ(xwTθj−1w)djw=1

　　　　那么对于某一个目标输出词ww ,其最大似然为：

∏j=2lwP(dwj|x**w,θwj−1)=∏j=2l**w[σ(xTwθw**j−1)]1−dwj[1−σ(xTwθw**j−1)]dwj∏j=2lwP(djw|xw,θj−1w)=∏j=2lw[σ(xwTθj−1w)]1−djw[1−σ(xwTθj−1w)]djw

　　　　在word2vec中，由于使用的是随机梯度上升法，所以并没有把所有样本的似然乘起来得到真正的训练集最大似然，仅仅每次只用一个样本更新梯度，这样做的目的是减少梯度计算量。这样我们可以得到ww 的对数似然函数LL 如下：

L=log∏j=2lwP(dwj|x**w,θwj−1)=∑j=2l**w((1−dwj)log[σ(xTwθw**j−1)]+dwjlo**g[1−σ(xTwθw**j−1)])L=log∏j=2lwP(djw|xw,θj−1w)=∑j=2lw((1−djw)log[σ(xwTθj−1w)]+djwlog[1−σ(xwTθj−1w)])

　　　　要得到模型中ww 词向量和内部节点的模型参数θθ , 我们使用梯度上升法即可。首先我们求模型参数θwj−1θj−1w 的梯度：

∂L∂θwj−1=(1−dwj)(σ(xTwθw**j−1)(1−σ(xTwθw**j−1)σ(xTwθw**j−1)x**w−dwj(σ(xTwθw**j−1)(1−σ(xTwθw**j−1)1−σ(xTwθw**j−1)x**w=(1−dwj)(1−σ(xTwθw**j−1))x**w−dwj**σ(xTwθw**j−1)x**w=(1−dwj−σ(xTwθw**j−1))x**w(1)(2)(3)(1)∂L∂θj−1w=(1−djw)(σ(xwTθj−1w)(1−σ(xwTθj−1w)σ(xwTθj−1w)xw−djw(σ(xwTθj−1w)(1−σ(xwTθj−1w)1−σ(xwTθj−1w)xw(2)=(1−djw)(1−σ(xwTθj−1w))xw−djwσ(xwTθj−1w)xw(3)=(1−djw−σ(xwTθj−1w))xw

　　　　如果大家看过之前写的逻辑回归原理小结，会发现这里的梯度推导过程基本类似。

　　　　同样的方法，可以求出x**wxw 的梯度表达式如下：

∂L∂x**w=∑j=2l**w(1−dwj−σ(xTwθw**j−1))θwj−1∂L∂xw=∑j=2lw(1−djw−σ(xwTθj−1w))θj−1w

　　　　有了梯度表达式，我们就可以用梯度上升法进行迭代来一步步的求解我们需要的所有的θwj−1θj−1w 和x**wxw 。

3. 基于Hierarchical Softmax的CBOW模型

　　　　由于word2vec有两种模型：CBOW和Skip-Gram,我们先看看基于CBOW模型时， Hierarchical Softmax如何使用。

　　　　首先我们要定义词向量的维度大小MM ，以及CBOW的上下文大小2c2c ,这样我们对于训练样本中的每一个词，其前面的cc 个词和后面的cc 个词作为了CBOW模型的输入,该词本身作为样本的输出，期望softmax概率最大。

　　　　在做CBOW模型前，我们需要先将词汇表建立成一颗霍夫曼树。

　　　　对于从输入层到隐藏层（投影层），这一步比较简单，就是对ww 周围的2c2c 个词向量求和取平均即可，即：

x**w=12c∑i=12cxixw=12c∑i=12cxi

　　　　第二步，通过梯度上升法来更新我们的θwj−1θj−1w 和x**wxw ，注意这里的x**wxw 是由2c2c 个词向量相加而成，我们做梯度更新完毕后会用梯度项直接更新原始的各个x**i(i=1,2,,,,2c)xi(i=1,2,,,,2c) ，即：

θwj−1=θwj−1+η(1−dwj−σ(xTwθw**j−1))x**wθj−1w=θj−1w+η(1−djw−σ(xwTθj−1w))xw

x**i=x**i+η∑j=2l**w(1−dwj−σ(xTwθw**j−1))θwj−1(i=1,2..,2c)xi=xi+η∑j=2lw(1−djw−σ(xwTθj−1w))θj−1w(i=1,2..,2c)

　　　　其中ηη 为梯度上升法的步长。

　　　　这里总结下基于Hierarchical Softmax的CBOW模型算法流程，梯度迭代使用了随机梯度上升法：

　　　　输入：基于CBOW的语料训练样本，词向量的维度大小MM ，CBOW的上下文大小2c2c ,步长ηη

　　　　输出：霍夫曼树的内部节点模型参数θθ ，所有的词向量ww

　　　　1. 基于语料训练样本建立霍夫曼树。

　　　　2. 随机初始化所有的模型参数θθ ，所有的词向量ww

　　　　3. 进行梯度上升迭代过程，对于训练集中的每一个样本(context(w),w)(context(w),w) 做如下处理：

　　　　　　a) e=0， 计算x**w=12c∑i=12cxixw=12c∑i=12cxi

　　　　　　b) for j = 2 to l**wlw , 计算：

f=σ(xTwθw**j−1)f=σ(xwTθj−1w)

g=(1−dwj−f)ηg=(1−djw−f)η

e=e+gθw**j−1e=e+gθj−1w

θwj−1=θwj−1+gxwθj−1w=θj−1w+gxw

　　　 c) 对于context(w)context(w) 中的每一个词向量x**ixi (共2c个)进行更新：

x**i=x**i+exi=xi+e

　　　　　　d) 如果梯度收敛，则结束梯度迭代，否则回到步骤3继续迭代。

4. 基于Hierarchical Softmax的Skip-Gram模型

　　　　现在我们先看看基于Skip-Gram模型时， Hierarchical Softmax如何使用。此时输入的只有一个词ww ,输出的为2c2c 个词向量context(w)context(w) 。

　　　　我们对于训练样本中的每一个词，该词本身作为样本的输入， 其前面的cc 个词和后面的cc 个词作为了Skip-Gram模型的输出,，期望这些词的softmax概率比其他的词大。

　　　　Skip-Gram模型和CBOW模型其实是反过来的，在上一篇已经讲过。

　　　　在做CBOW模型前，我们需要先将词汇表建立成一颗霍夫曼树。

　　　　对于从输入层到隐藏层（投影层），这一步比CBOW简单，由于只有一个词，所以，即x**wxw 就是词ww 对应的词向量。

　　　　第二步，通过梯度上升法来更新我们的θwj−1θj−1w 和x**wxw ，注意这里的x**wxw 周围有2c2c 个词向量，此时如果我们期望P(x**i|x**w),i=1,2…2cP(xi|xw),i=1,2…2c 最大。此时我们注意到由于上下文是相互的，在期望P(x**i|x**w),i=1,2…2cP(xi|xw),i=1,2…2c 最大化的同时，反过来我们也期望P(x**w|x**i),i=1,2…2cP(xw|xi),i=1,2…2c 最大。那么是使用P(x**i|x**w)P(xi|xw) 好还是P(x**w|x**i)P(xw|xi) 好呢，word2vec使用了后者，这样做的好处就是在一个迭代窗口内，我们不是只更新x**wxw 一个词，而是x**i,i=1,2…2cxi,i=1,2…2c 共2c2c 个词。这样整体的迭代会更加的均衡。因为这个原因，Skip-Gram模型并没有和CBOW模型一样对输入进行迭代更新，而是对2c2c 个输出进行迭代更新。

　　　　这里总结下基于Hierarchical Softmax的Skip-Gram模型算法流程，梯度迭代使用了随机梯度上升法：

　　　　输入：基于Skip-Gram的语料训练样本，词向量的维度大小MM ，Skip-Gram的上下文大小2c2c ,步长ηη

　　　　输出：霍夫曼树的内部节点模型参数θθ ，所有的词向量ww

　　　　1. 基于语料训练样本建立霍夫曼树。

　　　　2. 随机初始化所有的模型参数θθ ，所有的词向量ww ,

　　　　3. 进行梯度上升迭代过程，对于训练集中的每一个样本(w,context(w))(w,context(w)) 做如下处理：

　　　　　　a) for i =1 to 2c:

　　　　　　　　i) e=0

　　　　　　　　ii)for j = 2 to l**wlw , 计算：

f=σ(xTiθw**j−1)f=σ(xiTθj−1w)

g=(1−dwj−f)ηg=(1−djw−f)η

e=e+gθw**j−1e=e+gθj−1w

θwj−1=θwj−1+gxiθj−1w=θj−1w+gxi iii)

x**i=x**i+exi=xi+e

　　　　　　b)如果梯度收敛，则结束梯度迭代，算法结束，否则回到步骤a继续迭代。

5. Hierarchical Softmax的模型源码和算法的对应　　　　

　　　　这里给出上面算法和word2vec源码中的变量对应关系。

　　　　在源代码中，基于Hierarchical Softmax的CBOW模型算法在435-463行，基于Hierarchical Softmax的Skip-Gram的模型算法在495-519行。大家可以对着源代码再深入研究下算法。

　　　　在源代码中，neule对应我们上面的ee , syn0对应我们的x**wxw , syn1对应我们的θij−1θj−1i , layer1_size对应词向量的维度，window对应我们的cc 。

　　　　另外，vocab[word].code[d]指的是，当前单词word的，第d个编码，编码不含Root结点。vocab[word].point[d]指的是，当前单词word，第d个编码下，前置的结点。

　　

　

发表于
字数统计: | 阅读时长 ≈

神经网络基础

1.神经网络模型

所谓神经网络就是将许多个单一“神经元”联结在一起，这样，一个“神经元”的输出就可以是另一个“神经元”的输入。例如，下图就是一个简单的神经网络：

我们使用圆圈来表示神经网络的输入，标上“+1”的圆圈被称为”’偏置节点”’，也就是截距项。神经网络最左边的一层叫做 ”‘输入层”’，最右的一层叫做”‘输出层’”（本例中，输出层只有一个节点）。中间所有节点组成的一层叫做”’隐藏层”’，因为我们不能在训练样本集中观测到它们的值。同时可以看到，以上神经网络的例子中有3个”’输入单元”’（偏置单元不计在内），3个”’隐藏单元”’及一个”’输出单元”’。

我们用nl 来表示网络的层数，本例中nl=3，我们将第l 层记为Ll ，于是L1是输入层，输出层Lni 。本例神经网络有参数(W,b)=(W(1),b(1),W(2),b(2)) ，其中W(l)ij（下面的式子中用到）是第l层第j 单元与第l+1 层第i 单元之间的联接参数（其实就是连接线上的权重，注意标号顺序），bi(l) 是第l+1 层第i 单元的偏置项。因此在本例中，W(1)∈ℜ3×3 ，W(2)∈ℜ1×3 。注意，没有其他单元连向偏置单元(即偏置单元没有输入)，因为它们总是输出+1。同时，我们用sl表示第ll 层的节点数（偏置单元不计在内）。

本例神经网络的计算步骤如下:

我们用z(l)i 表示第l 层第i单元输入加权和（包括偏置单元）:

再将激活函数进行广播,及可以得到前向传播过程：

当然神经网络也可以具有多个隐藏层，其计算原理同之前类似。

如果你想预测的输出是多个的，那这种神经网络很适用。（比如，在医疗诊断应用中，患者的体征指标就可以作为向量的输入值，而不同的输出值y**iyi 可以表示不同的疾病存在与否。）

2.前馈神经网络(FF)

前馈神经网络（FF），这是一个很古老的方法——这种方法起源于50年代。它的工作原理通常遵循以下规则：

1.所有节点都完全连接

2.激活从输入层流向输出，无回环

3.输入和输出之间有一层（隐含层）

在大多数情况下，这种类型的网络使用反向传播方法进行训练。

3.感知机

1.算法原理

想法来自生物学的神经元的一些工作方式，多个生物信号 (input singals) 到达树突 (dentrites)并进入细胞核 (cell nucleus)，如果这些信号的效果累加达到一个阈值，那么通过轴突 (axon) 产生一个输出信号 (output signals)。在有监督学习与分类的背景下，这样的算法可被用来预测一个样本是否属于某个类别。

正式地，我们可以把这个问题表述为一个二分类任务，并且为了简单起见，将这两个类别分别定义为 1 (正类) 与 -1（负类）。接着定义一个激活函数 (activation function) ,, 它输入的是 xx 与其对应的权重向量 ww 的一个线性组合.

对于一个指定样本 x(i)x(i), 如果 ϕ(z)ϕ(z) 的输出值大于预先定义的一个阈值 Θ, 那么就预测其类别 1. 否则，预测为类别 -1. 在感知器算法中，激活函数 是一个简单的单位阶跃函数 (unit step function)

需要注意一点的是只有当两个类别是线性可分时，感知器算法才能保证收敛。如果两个类别不是线性可分，那么我们可以在训练集上设置一个最大的迭代次数, 或是设置一个可接受的错误分类的阈值。

2.感知机权重的学习过程

采用随机梯度下降法：

推荐一个神经网络可视化的网站 :tensorflow 游乐场

3.使用tensoeflow定义几层简单的神经网络

激活函数使用sigmoid,递归使用链式法则来实现反向传播:

  1. 再次运用的时简单类定义进行神经网络的计算。

  2. tensorflow版本待更

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    91
    92
    93
    94
    95
    96
    97
    98
    99
    100
    101
    102
    103
    104
    105
    106
    107
    108
    109
    110
    111
    112
    113
    114
    115
    116
    117
    118
    119
    120
    121
    import numpy as np
    import math
    import random

    def rand(a,b):
        return (b-a)*random.random()+a

    def make_matrix(m,n,fill=0.0):
        mat=[]
        for i in range(m):
            mat.append([fill]*n)
        return mat

    def sigmoid(x):
        return 1.0/(1.0+math.exp(-x));

    def sigmod_derivate(x):
        return x*(1-x)

    class BPNeuralNetWork:
        
        def _init_(self):
            self.input_n=0
            self.hidden_n=0
            self.output_n=0
            self.input_cells=[]
            self.hidden_cells=[]
            self.output_cells=[]
            self.input_weights=[]
            self.output_weights=[]
            
        def setup(self,ni,nh,no):
            self.input_n=ni+1
            self.hidden_n=nh
            self.output_n=no
            
            self.input_cells=[1.0]*self.input_n
            self.hidden_cells=[1.0]*self.hidden_n
            self.output_cells=[1.0]*self.output_n
            
            self.input_weights=make_matrix(self.input_n,self.hidden_n)
            self.output_weights=make_matrix(self.hidden_n,self.output_n)
            for i in range(self.input_n):
                for h in range(self.hidden_n):
                    self.input_weights[i][h]=rand(-0.2,0.2)
            for h in range(self.hidden_n):
                for j in range(self.output_n):
                    self.output_weights[h][j]=rand(-0.2,0.2)

        def predict(self,inputs):
            for i in range(self.input_n-1.0):
                self.input_cells[i]=inputs[i]
                
            for j in range(self.hidden_n):
                total+=self.input_cells[i]*self.input_weights[i][j]
            self.hidden_cells[i]=sigmoid(total)#不要忘记去线性化
            
            for k in range(self.output_n):
                total=0.0
                for j in range(self.output_n):
                    total+=self.hidden_cells[j]*self.output_weights[j][k]
                    self.output_cells[k]=sigmoid(total)
            return self.output_cells[:]
        
        
        def back_propagate(self,case,label,learn):
            
            self.predict(case)
            
            output_deltas=[0.0]*self.output_n
            for k in range(self.output_n):
                error=label[k]-self.output_cells[k]
                output_deltas[k]=sigmod_derivate(self.output_cells[k])*error
                
            hidden_deltas=[0.0]*self.hidden_n
            for j in range(self.input_n):
                error=0.0
                for k in range(self.output_n):
                    error+=output_deltas[k]*self.output_weights[j][k]
                hidden_deltas[j]=sigmod_derivate(self.hidden_cells[j])*error
                
            for j in range(self.hidden_n):
                for k in range(self.output_n):
                    self.output_weights[j][k]+=learn*output_deltas[k]*self.hidden_cells[j]
            
            for i in range(self.input_n):
                for j in range(self.hidden_n):
                    self.input_weights[i][j]=learn*hidden_deltas[j]*self.input_cells[i]
                    
                    error=0
            
            for o in range(len(label)):
                #L1实现
                error+=0.5*(label[o]-self.output_cells[o])**2
            return error
        
        def train(self,cases,labels,limit=100,learn=0.05):
            for i in range(limit):
                error=0
                for i in range(len(cases)):
                    label=labels[i]
                    case=cases[i]
                    error+=self.back_propagate(case,label,learn)
                pass
            
        def test(self):
            cases=[
                [0,0],
                [0,1],
                [1,0],
                [1,1],
            ]
            labels=[[0],[1],[1],[0]]
            dself.setup(2,5,1)
            self.train(cases,labels,10000,0.05)
            for case in cases:
                print(self.predict(case))
                
    if __name__=='__mian__':
        nn=BPNeuralNetWork()
        nn.test()

4.激活函数的种类以及各自的背景，优缺点

1,定义

在神经元中，输入的 inputs 通过加权，求和后，还被作用了一个函数，这个函数就是激活函数 Activation Function。

使用激活函数对线性值进行去线性化。

2.为什么要使用激活函数(线性模型的局限性)

如果不用激励函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合。如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中

3.分类定义
(1).sigmoid函数

公式：

曲线:

取值范围为(0,1)，用于隐层神经元输出。
它可以将一个实数映射到(0,1)的区间，可以用来做二分类。
在特征相差比较复杂或是相差不是特别大时效果比较好。
sigmoid缺点：

激活函数计算量大，反向传播求误差梯度时，求导涉及除法。反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练。

(2) Tanh函数

公式：

曲线:

也称为双切正切函数
取值范围为[-1,1]。
tanh在特征相差明显时的效果会很好，在循环过程中会不断扩大特征果。与 sigmoid 的区别是，tanh 是 0 均值的，因此实际应用中 tanh 会比 sigmoid 更好。

3) ReLU

Rectified Linear Unit(ReLU) - 用于隐层神经元输出

公式：

曲线

输入信号 <0 时，输出都是0，="">0 的情况下，输出等于输入

ReLU 的优点：使用 ReLU 得到的 SGD 的收敛速度会比 sigmoid/tanh 快很多

ReLU 的缺点：
训练的时候很”脆弱”，很容易就”die”了
例如，一个非常大的梯度流过一个 ReLU 神经元，更新过参数之后，这个神经元再也不会对任何数据有激活现象了，那么这个神经元的梯度就永远都会是 0.
如果 learning rate 很大，那么很有可能网络中的 40% 的神经元都”dead”了。

5.深度学习中的正则化

1.定义

《统计学习方法》中认为正则化是选择模型的一种方法。

正则化通过对学习算法的修改，旨在减少泛化误差而不是训练误差。目前有很多正则化策略，有些是向机器学习模型中添加限制参数值的额外约束，有些是向目标函数添加额外项来对参数值进行软约束。

2.L1正则化

L1正则化对梯度的影响不是线性地缩放每个wi而是添加了一项与sign(wi)同号的常数。这种形式的梯度不一定能得到直接算术解。

相比L2正则化，L1正则化会产生更稀疏的解。这种稀疏性广泛用于特征选择机制，可以从可用的特征子集中选择出有意义的特征，化简机器学习问题。

L1正则化可通过假设权重w的先验分布为拉普拉斯分布，由最大后验概率估计导出.

3.L2正则化

通过向目标函数添加一个L2范数平方项，使权重更加接近原点。

《Deep Learning》书中也提到：L2正则化能让学习算法“感知”到具有较高方差的输入xx，因此与输出目标的协方差较小的特征的权重将会收缩。L2正则化能够很好的防止过拟合：

  1. 通过引入L2正则，使模型参数偏好比较小的值，这其实也限制的函数空间的大小，有针对的减小了模型容量。一般来说，大的参数值对应于波动剧烈的函数，小的参数值对应于比较平缓的参数，因为小参数对于输入的改变不会那么敏感。发生过拟合往往是因为顾及到了所有样本点，所以此时的函数波动会比较大，如下面右图所示。过拟合的模型往往具有比较大的参数，如果将这部分模型族从假设空间中剔除掉，发生过拟合的可能就变小。

​

  1. L2正则化能让学习算法“感知”到具有较高方差的输入xx，因此与输出目标的协方差较小的特征的权重将会收缩。因此L2正则化总是倾向于对那些训练集样本共用的特征产生较大的响应，而减小对个别样本独有的特征产生的响应。因此L2正则有抑制那些“独有特征”的作用，这在一定程度上也减小了过拟合的风险。
    　　L2正则化可通过假设权重ww的先验分布为高斯分布，由最大后验概率估计导出.
4.数据集增强
  • 原因：一般而言，比较成功的神经网络需要大量的参数，许许多多的神经网路的参数都是数以百万计，而使得这些参数可以正确工作则需要大量的数据进行训练，而实际情况中数据并没有我们想象中的那么多
  • 作用：
    1. 增加训练的数据量，提高模型的泛化能力
    2. 增加噪声数据，提升模型的鲁棒性
  • 方法：
    1. 增加数据集，一般较难实现
    2. 利用已有的数据比如翻转、平移或旋转，创造出更多的数据，来使得神经网络具有更好的泛化效果。
  • 分类：
    1. 离线增强 ： 直接对数据集进行处理，数据的数目会变成增强因子 x 原数据集的数目 ，这种方法常常用于数据集很小的时候
    2. 在线增强 ： 这种增强的方法用于，获得 batch 数据之后，然后对这个 batch 的数据进行增强，如旋转、平移、翻折等相应的变化，由于有些数据集不能接受线性级别的增长，这种方法长用于大的数据集，很多机器学习框架已经支持了这种数据增强方式，并且可以使用 GPU 优化计算。
5.噪声增加

​ 简单提高网络抗噪能力的方法，就是在训练中加入随机噪声一起训练。我们可以在网络的不同位置加入噪声：输入层，隐藏层，输出层。
　　数据集增强在某种意义上也能看做是在输入层加入噪声，通过随机旋转、翻转，色彩变换，裁剪等操作人工扩充训练集大小。这样可以使得网络对于输入更加鲁棒。
　　当然如果你能保证数据集没错误，不向输出层加入噪声也没关系。解决这个问题常见的办法是标签平滑，通过把确切的分类目标从0和1替换成ϵk−1和1−ϵ，正则化具有k个输出的softmax函数的模型。标签平滑的优势是能够防止模型追求确切的概率而不能学习正确分类。
　　从优化过程的角度来看，对权重叠加方差极小噪声等价于对权重是假范数惩罚，可以被解释为关于权重的贝叶斯推断的随即实现（这一点我不是很理解）。换个角度就很结论就很明朗了，因为我们在权重中添加了一些随机扰动，这鼓励优化过程找到一个参数空间，该空间对微小参数变化引起的输出变化影像很小。将模型送入了一个对于微小变化不敏感的区域，不仅找到了最小值，还找到了一个宽扁的最小值区域。

early stop（提前终止)

模型过拟合一般是发生在训练次数过多的情况下，那么只要我们在过拟合之前停止训练即可。这也是深度学习中最常用的正则化形式，主要是因为它的有效性和简单性。提前终止需要验证集损失作为观测指标，当验证集损失开始持续上升时，这时就该停止训练过程了。

Dropout

先介绍集成学习的概念

  • 集成学习通过结合几个模型降低泛化误差的技术。分别训练几个不同的模型，然后让所有模型表决测试样例的输出，也被称为模型平均。模型平均奏效的原因是不同的模型通常不会再测试集上产生完全相同的误差。

    假设我们有k个回归模型，每个模型在每个例子上的误差为ϵi，这个误差服从均值为0，方差E[ϵi^2]=v且协方差E[ϵiϵj]=c的多维正态分布。通过所有集成模型的平均预测所得误差是1k∑iϵi，则该集成预测期的平方误差的期望为：

​ 在误差完全相关即c=v的情况下，E[(1/k*∑iϵi)^2]=v，模型平均对提升结果没有任何帮 助；在误差完全不想关即c=0的情况下，集成模型的误差期望为E[(1/k∑iϵi)^2]=(1/k)v。用一 句话说，平均上，集成至少与它任何成员表现的一样好，并且如果成员误差是独立的，集成将显著地比其成员表现的更好。神经网络中随机初始化的差异、小批量的随机选择、超参数的差异或不同输出的非确定性实现往往足以使得集成中的不同成员具有部分独立的误差。

  • Dropout

    Dropout是每次训练过程中随机舍弃一些神经元之间的连接

Dropout提供了一种廉价的Bagging集成近似，能够训练和评估指数级数量的神经网络。Dropout和Bagging训练不太一样，Bagging所有模型都是独立的，而Dropout是所有模型共享参数，每个模型集成父神经网络参数的不同子集，这中参数共享的方式使得在有限可用内存下表示指数级数量的模型变得可能。
　　隐藏单元经过Dropout训练后，它必须学习与不同采样神经元的合作，使得神经元具有更强的健壮性，并驱使神经元通过自身获取到有用的特征，而不是依赖其他神经元去纠正自身的错误。这可以看错对输入内容的信息高度智能化，自适应破坏的一种形式，而不是对输入原始值的破坏。
　　Dropout的另一个重要方面是噪声是乘性的。如果是固定规模的加性噪声，那么加了噪声ϵ的ReLU可以简单的学会使hi变得很大（使增加的噪声ϵϵ变得不显著）。乘性噪声就不允许这样病态的去解决噪声鲁棒问题。

深度模型的优化

1.参数初始化策略

1.梯度下降算法

  • 批量梯度下降(Batch gradient descent)

    批量梯度下降每次学习都使用整个训练集，因此其优点在于每次更新都会朝着正确的方向进行，最后能够保证收敛于极值点(凸函数收敛于全局极值点，非凸函数可能会收敛于局部极值点)，但是其缺点在于每次学习时间过长，并且如果训练集很大以至于需要消耗大量的内存，并且全量梯度下降不能进行在线模型参数更新。

  • 随机梯度下降(Stochastic gradient descent)

    随机梯度下降算法每次从训练集中随机选择一个样本来进行学习，即： θ=θ−η⋅∇θJ(θ;xi;yi)

    批量梯度下降算法每次都会使用全部训练样本，因此这些计算是冗余的，因为每次都使用完全相同的样本集。而随机梯度下降算法每次只随机选择一个样本来更新模型参数，因此每次的学习是非常快速的，并且可以进行在线更新。

    随机梯度下降最大的缺点在于每次更新可能并不会按照正确的方向进行，因此可以带来优化波动(扰动)

  • 小批量梯度下降(Mini-batch gradient descent)

    Mini-batch 梯度下降综合了 batch 梯度下降与 stochastic 梯度下降，在每次更新速度与更新次数中间取得一个平衡，其每次更新从训练集中随机选择 m,m<n 个样本进行学习，mini-batch梯度下降可以保证收敛性，常用于神经网络中。

以下摘抄自网络:参数初始化策略
2.AdaGrad

AdaGrad 算法，如下图所示，独立地适应所有模型参数的学习率，缩放每个参数反比于其所有梯度历史平方值总和的平方根 (Duchi et al., 2011)。具有损失最大偏导的参数相应地有一个快速下降的学习率，而具有小偏导的参数在学习率上有相对较小的下降。净效果是在参数空间中更为平缓的倾斜方向会取得更大的进步。在凸优化背景中， AdaGrad 算法具有一些令人满意的理论性质。然而，经验上已经发现，对于训练深度神经网络模型而言， 从训练开始时积累梯度平方会导致有效学习率过早和过量的减小。 AdaGrad 在某些深度学习模型上效果不错，但不是全部

1.RMSProp

RMSProp 算法 (Hinton, 2012) 修改 AdaGrad 以在非凸设定下效果更好，改
变梯度积累为指数加权的移动平均。 AdaGrad 旨在应用于凸问题时快速收敛。当应用于非凸函数训练神经网络时，学习轨迹可能穿过了很多不同的结构，最终到达一个局部是凸碗的区域。 AdaGrad 根据平方梯度的整个历史收缩学习率，可能使得学习率在达到这样的凸结构前就变得太小了。 RMSProp 使用指数衰减平均以丢弃遥远过去的历史，使其能够在找到凸碗状结构后快速收敛，它就像一个初始化于该碗状结构的 AdaGrad 算法实例。RMSProp 的标准形式如算法 8.5 所示，结合 Nesterov 动量的形式如算法 8.6 所示。相比于 AdaGrad，使用移动平均引入了一个新的超参数ρ，用来控制移动平均的长度范围。经验上， RMSProp 已被证明是一种有效且实用的深度神经网络优化算法。目前它是深度学习从业者经常采用的优化方法之一。

4.Adam

Adam (Kingma and Ba, 2014) 是另一种学习率自适应的优化算法，如算法 8.7 所示。 “Adam’’ 这个名字派生自短语 “adaptive moments’’。早期算法背景下，它也许最好被看作结合 RMSProp 和具有一些重要区别的动量的变种。首先，在 Adam 中，动量直接并入了梯度一阶矩（指数加权）的估计。将动量加入 RMSProp 最直观的方法是将动量应用于缩放后的梯度。结合缩放的动量使用没有明确的理论动机。其次， Adam 包括偏置修正，修正从原点初始化的一阶矩（动量项）和（非中心的）二阶矩的估计（算法 8.7 ）。 RMSProp 也采用了（非中心的）二阶矩估计，然而缺失了修正因子。因此，不像 Adam，RMSProp 二阶矩估计可能在训练初期有很高的偏置。Adam 通常被认为对超参数的选择相当鲁棒，尽管学习率有时需要从建议的默认修改。

2.batch normal层
3.layer normal层

发表于
字数统计: | 阅读时长 ≈

1.共轭先验分布

共轭先验分布的提出：某观测数据服从概率分布p(θ），当观测到新的数据时，思考下列问题：

1.能否根据新观测数据X更新参数θ；
2.根据新观测的数据可以在多大的程度上改变参数θ：θ=θ+rθ；
3.当重新估计得到θ时，给出的新参数数值θ的新概率分布p(θ|x)；

分析：根据贝叶斯公式：p(θ|x)=p(x|θ)p(θ)
p(x),其中p(x|θ)是在已知θ的情况下估计x的概率分布，又称似然函数；p(θ)是原有的θ的概率分布；要想利用观测到的数据更新参数θ，就要使更新后的p(θ|x)和p(θ)服从相同的分布，所以p(θ)和p(θ|x)形成共轭分布，p(θ)叫做p(θ|x)的共轭先验分布。
举个投硬币的例子：使用参数θ的伯努利模型，θ为正面的概率，则结果为x的概率分布为：p(x|θ)=θx(1−θ)1-x

在贝叶斯概率理论中，如果后验概率P(θ|X)和先验概率P(θ)满足同样的分布律(形式相同，参数不同)。那么，先验分布和后验分布被叫做共轭分布，同时，先验分布叫做似然函数的共轭先验分布。

2.pLSA

LSA是处理这类问题的著名技术。其主要思想就是映射高维向量到潜在语义空间，使其降维。LSA的目标就是要寻找到能够很好解决实体间词法和语义关系的数据映射。正是由于这些特性，使得LSA成为相当有价值并被广泛应用的分析工具。PLSA是以统计学的角度来看待LSA，相比于标准的LSA，他的概率学变种有着更巨大的影响。

概率潜在语义分析（pLSA） 基于双模式和共现的数据分析方法延伸的经典的统计学方法。

概率潜在语义分析应用于信息检索，过滤，自然语言处理，文本的机器学习或者其他相关领域。概率潜在语义分析与标准潜在语义分析的不同是，标准潜在语义分析是以共现表（就是共现的矩阵）的奇异值分解的形式表现的，而概率潜在语义分析却是基于派生自LCM的混合矩阵分解。考虑到word和doc共现形式，概率潜在语义分析基于多项式分布和条件分布的混合来建模共现的概率。所谓共现其实就是W和D的一个矩阵，所谓双模式就是在W和D上同时进行考虑。

PLSA有时会出现过拟合的现象。所谓过拟合（Overfit），是这样一种现象：一个假设在训练数据上能够获得比其他假设更好的拟合，但是在训练数据外的数据集上却不能很好的拟合数据。此时我们就叫这个假设出现了overfit的现象。出现这种现象的主要原因是训练数据中存在噪音或者训练数据太少。

解决办法，要避免过拟合的问题，PLSA使用了一种广泛应用的最大似然估计的方法，期望最大化。PLSA中训练参数的值会随着文档的数目线性递增。PLSA可以生成其所在数据集的的文档的模型，但却不能生成新文档的模型。

数学推导待补充（看不懂…..)

3.LDA主题模型原理

待补充（看不懂…..)

4.LDA参数学习–Gibbs采样训练流程

  1. 选择合适的主题数K，选择合适的超参数α、η；
  2. 对于语料库中每一篇文档的每一个词，随机的赋予一个主题编号z；
  3. 重新扫描语料库，对于每一个词，利用Gibbs采样公式更新它的topic的编号，并更新语料库中该词的编号。
  4. 重复第三步中基于坐标轴轮询的Gibbs采样，直到Gibbs采样收敛。
  5. 统计语料库中各个文档各个词的主题，得到文档主题分布

5.LDA生成主题特征，在之前的特征的基础上加入主题特征实现文本分类

1.先来了解数据集

数据集位于lda安装目录的tests文件夹中，包含三个文件：reuters.ldac, reuters.titles, reuters.tokens。
reuters.titles包含了395个文档的标题
reuters.tokens包含了这395个文档中出现的所有单词，总共是4258个
reuters.ldac有395行，第i行代表第i个文档中各个词汇出现的频率。以第0行为例，第0行代表的是第0个文档，从reuters.titles中可查到该文档的标题为“UK: Prince Charles spearheads British royal revolution. LONDON 1996-08-20”。
第0行的数据为：
159 0:1 2:1 6:1 9:1 12:5 13:2 20:1 21:4 24:2 29:1 ……
第一个数字159表示第0个文档里总共出现了159个单词（每个单词出现一或多次），
0:1表示第0个单词出现了1次，从reuters.tokens查到第0个单词为church
2:1表示第2个单词出现了1次，从reuters.tokens查到第2个单词为years
6:1表示第6个单词出现了1次，从reuters.tokens查到第6个单词为told
9:1表示第9个单词出现了1次，从reuters.tokens查到第9个单词为year
12:5表示第12个单词出现了5次，从reuters.tokens查到第12个单词为charles
……
这里第1、3、4、5、7、8、10、11……个单词序号和次数没列出来，表示出现的次数为0
注意：
395个文档的原文是没有的。上述三个文档是根据这395个文档处理之后得到的。

2代码实现
1
2
3
4
5
6
7
8
9
10
#查看文本中词出先的频率
import numpy as np
import lda
import lda.datasets

X=lda.datasets.load_reuters()
print("type(X):{}".format(type(X)))
print("shape:{}\n".format(X.shape))

print(X[:5,:5])

1
2
3
4
5
#查看词
vocab=lda.datasets.load_reuters_vocab()
print("type(vocab):{}".format(type(vocab)))
print("len(vocab):{}\n".format(len(vocab)))
print(vocab[:5])

1
2
3
4
5
#查看文档标题
titles=lda.datasets.load_reuters_titles()
print("type(title):{}".format(type(titles)))
print("len(titles):{}".format(len(titles)))
print(titles[:5])

1
2
3
4
5
6
7
8
9
#查看前五个文档第0个词出现的次数
doc_id=0
word_id=0
while doc_id <5:
    print("doc id:{} word id:{}".format(doc_id,word_id))
    print("--count:{}".format(X[doc_id,word_id]))#doc_id是文档的标记
    print("--word:{}".format(vocab[word_id]))
    print("--doc :{}\n".format(titles[doc_id]))
    doc_id+=1

1
2
3
#训练模型
model=lda.LDA(n_topics=20,n_iter=500,random_state=1)
model.fit(X)

#主题-单词分布

#计算前三个单词在所有的主题中所占的权重
topic_word=model.topic_word_
print(“type(topic_word):{}”.format(type(topic_word)))
print(“shape:{}”.format(topic_word.shape))
print(vocab[:3])
print(topic_word[:,:3])

1
2
3
4
#计算所有行的比重之和
for n in range(20):
    sum_pr=sum(topic_word[n,:])
    print("topic:{} sum:{}".format(n,sum_pr))

1
2
3
4
5
#计算各个主题的topN个词
n=5
for i,topic_dist in enumerate(topic_word):
    topic_words=np.array(vocab)[np.argsort(topic_dist)[:-(n+1):-1]]
    print("top {}\n- {}".format(i,' '.join(topic_words)))

1
2
3
4
5
6
7
8
#计算前十篇文章最有可能的主题

doc_topic=model.doc_topic_
print("ytpr(doc_topic):{}".format(type(doc_topic)))
print("shape:{}".format(doc_topic.shape))
for n in range(10):
    topic_most_pr=doc_topic[n].argmax()
    print("doc:{} topic :{}".format(n,topic_most_pr))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#可视化分析
#绘制主题0，5，9，14的词的出现次数

import matplotlib.pyplot as plt

f,ax=plt.subplots(5,1,figsize=(8,6),sharex=True)
for i,k in enumerate([0,5,9,14,19]):#枚举
    print(i,k)
    ax[i].stem(topic_word[k,:],linefmt='b-', markerfmt='bo', basefmt='w-')
    
    ax[i].set_xlim(-50, 4350)
    ax[i].set_ylim(0, 0.08)
    ax[i].set_ylabel("Prob")
    ax[i].set_title("topic {}".format(k))
ax[4].set_xlabel("word")

plt.tight_layout()
plt.show()

发表于
字数统计: | 阅读时长 ≈

支持向量机（SVM）原理及应用

1.算法原理

1.简介

支持向量机（support vector machines）是一种二分类模型，它的目的是寻找一个超平面来对样本进行分割，分割的原则是间隔最大化，最终转化为一个凸二次规划问题来求解。由简至繁的模型包括：

  • 当训练样本线性可分时，通过硬间隔最大化，学习一个线性可分支持向量机；
  • 当训练样本近似线性可分时，通过软间隔最大化，学习一个线性支持向量机；
  • 当训练样本线性不可分时，通过核技巧和软间隔最大化，学习一个非线性支持向量机；

2. 线性可分的支持向量机

基本的想法就是基于训练集D在样本空间中找到一个划分超平面，将不同类别的样本分开。训练集标签为yi={1|-1}

直观看上去，能将训练样本分开的划分超平面有很多，但应该去找位于两类训练样本“正中间”的划分超平面，即图6.1中红色的那条，因为该划分超平面对训练样本局部扰动的“容忍”性最好，例如，由于训练集的局限性或者噪声的因素，训练集外的样本可能比图6.1中的训练样本更接近两个类的分隔界，这将使许多划分超平面出现错误。而红色超平面的影响最小，简言之，这个划分超平面所产生的结果是鲁棒性的。

那什么是线性可分呢？

如果一个线性函数能够将样本分开，称这些数据样本是线性可分的。那么什么是线性函数呢？其实很简单，在二维空间中就是一条直线，在三维空间中就是一个平面，以此类推，如果不考虑空间维数，这样的线性函数统称为超平面。我们看一个简单的二维空间的例子，O代表正类，X代表负类，样本是线性可分的，但是很显然不只有这一条直线可以将样本分开，而是有无数条，我们所说的线性可分支持向量机就对应着能将数据正确划分并且间隔最大的直线。

在实际应用总，我们所要求解的是能将数据正确划分的并且间隔最大的超平面
一个点距离超平面的远近可以表示分类的确信度，，距离超平面更远的点确信度更高，求解最号的SVM时，我们不许考录所有点，只要让超平面距离较近的点的点间隔最大即可

距离超平面最近的几个点成为“支持向量”，两条虚线的距离称为 * 间隔 *

间隔的计算：两个异类支持向量在实现的法线方向的投影大小

3.非线性支持向量机和核函数

待补充

4.线性支持向量机（软间隔支持向量机）与松弛变量

待补充

2.SVM优缺点

优点：
1、使用核函数可以向高维空间进行映射
2、使用核函数可以解决非线性的分类
3、分类思想很简单，就是将样本与决策面的间隔最大化
4、分类效果较好
缺点：
1、对大规模数据训练比较困难
2、无法直接支持多分类，但是可以使用间接的方法来做

3.SVM应用场景

SVM在很多数据集上都有优秀的表现。
相对来说，SVM尽量保持与样本间距离的性质导致它抗攻击的能力更强。
和随机森林一样，这也是一个拿到数据就可以先尝试一下的算法

4.SVM sklearn参数学习

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class sklearn.svm.SVC(
            C=1.0, 
            kernel='rbf', 
            degree=3, 
            gamma='auto', 
            coef0=0.0, 
            shrinking=True, 
            probability=False, 
            tol=0.001, 
            cache_size=200, 
            class_weight=None, 
            verbose=False, 
            max_iter=-1, 
            decision_function_shape='ovr', 
            random_state=None)
  • SVC　class sklearn.svm.`SVC`(C=1.0, kernel=’rbf’, degree=3, gamma=’auto’, coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape=’ovr’, random_state=None)　

　　**C:**惩罚系数，用来控制损失函数的惩罚系数，类似于LR中的正则化系数。C越大，相当于惩罚松弛变量，希望松弛变量接近0，即对误分类的惩罚增大，趋向于对训练集全分对的情况，这样会出现训练集测试时准确率很高，但泛化能力弱，容易导致过拟合。 C值小，对误分类的惩罚减小，容错能力增强，泛化能力较强，但也可能欠拟合。

　　**kernel:**算法中采用的和函数类型，核函数是用来将非线性问题转化为线性问题的一种方法。参数选择有RBF, Linear, Poly, Sigmoid，precomputed或者自定义一个核函数, 默认的是”RBF”，即径向基核，也就是高斯核函数；而Linear指的是线性核函数，Poly指的是多项式核，Sigmoid指的是双曲正切函数tanh核；。

　　degree: 当指定kernel为’poly’时，表示选择的多项式的最高次数，默认为三次多项式；若指定kernel不是’poly’，则忽略，即该参数只对’poly’有用。（多项式核函数是将低维的输入空间映射到高维的特征空间）

　　**gamma:**核函数系数，该参数是rbf，poly和sigmoid的内核系数；默认是’auto’，那么将会使用特征位数的倒数，即1 / n_features。（即核函数的带宽，超圆的半径）。gamma越大，σ越小，使得高斯分布又高又瘦，造成模型只能作用于支持向量附近，可能导致过拟合；反之，gamma越小，σ越大，高斯分布会过于平滑，在训练集上分类效果不佳，可能导致欠拟合。

　　**coef0:**核函数常数值(y=kx+b中的b值)，只有‘poly’和‘sigmoid’核函数有，默认值是0。

　　shrinking : 是否进行启发式。如果能预知哪些变量对应着支持向量，则只要在这些样本上训练就够了，其他样本可不予考虑，这不影响训练结果，但降低了问题的规模并有助于迅速求解。进一步，如果能预知哪些变量在边界上(即a=C)，则这些变量可保持不动，只对其他变量进行优化，从而使问题的规模更小，训练时间大大降低。这就是Shrinking技术。 Shrinking技术基于这样一个事实：支持向量只占训练样本的少部分，并且大多数支持向量的拉格朗日乘子等于C。

　　probability: 是否使用概率估计，默认是False。必须在 fit( ) 方法前使用，该方法的使用会降低运算速度。

　　**tol:**残差收敛条件，默认是0.0001，即容忍1000分类里出现一个错误，与LR中的一致；误差项达到指定值时则停止训练。

　　**cache_size:**缓冲大小，用来限制计算量大小，默认是200M。

　　class_weight : {dict, ‘balanced’}，字典类型或者’balance’字符串。权重设置，正类和反类的样本数量是不一样的，这里就会出现类别不平衡问题，该参数就是指每个类所占据的权重，默认为1，即默认正类样本数量和反类一样多，也可以用一个字典dict指定每个类的权值，或者选择默认的参数balanced，指按照每个类中样本数量的比例自动分配权值。如果不设置，则默认所有类权重值相同，以字典形式传入。 将类i 的参数C设置为SVC的class_weight[i]C。如果没有给出，所有类的weight 为1。’balanced’模式使用y 值自动调整权重，调整方式是与输入数据中类频率成反比。如n_samples / (n_classes np.bincount(y))。（给每个类别分别设置不同的惩罚参数C，如果没有给，则会给所有类别都给C=1，即前面参数指出的参数C。如果给定参数’balance’，则使用y的值自动调整与输入数据中的类频率成反比的权重。）

　　verbose : 是否启用详细输出。在训练数据完成之后，会把训练的详细信息全部输出打印出来，可以看到训练了多少步，训练的目标值是多少；但是在多线程环境下，由于多个线程会导致线程变量通信有困难，因此verbose选项的值就是出错，所以多线程下不要使用该参数。

　　**max_iter:**最大迭代次数，默认是-1，即没有限制。这个是硬限制，它的优先级要高于tol参数，不论训练的标准和精度达到要求没有，都要停止训练。

　　decision_function_shape ： 原始的SVM只适用于二分类问题，如果要将其扩展到多类分类，就要采取一定的融合策略，这里提供了三种选择。‘ovo’ 一对一，为one v one，即将类别两两之间进行划分，用二分类的方法模拟多分类的结果，决策所使用的返回的是（样本数，类别数*(类别数-1)/2）； ‘ovr’ 一对多，为one v rest，即一个类别与其他类别进行划分，返回的是(样本数，类别数)，或者None，就是不采用任何融合策略。默认是ovr，因为此种效果要比oro略好一点。

　　random_state: 在使用SVM训练数据时，要先将训练数据打乱顺序，用来提高分类精度，这里就用到了伪随机序列。如果该参数给定的是一个整数，则该整数就是伪随机序列的种子值；如果给定的就是一个随机实例，则采用给定的随机实例来进行打乱处理；如果啥都没给，则采用默认的 np.random实例来处理。

  • NuSVC　　　　　　　　　　　　　　　　　class sklearn.svm.`NuSVC`(nu=0.5, kernel=’rbf’, degree=3, gamma=’auto’, coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape=’ovr’, random_state=None) 　

    　　nu： 训练误差部分的上限和支持向量部分的下限，取值在（0，1）之间，默认是0.5

  • LinearSVC　　　　class sklearn.svm.`LinearSVC`(penalty=’l2’, loss=’squared_hinge’, dual=True, tol=0.0001, C=1.0, multi_class=’ovr’, fit_intercept=True, intercept_scaling=1, class_weight=None, verbose=0, random_state=None, max_iter=1000)

　　**penalty:**正则化参数，L1和L2两种参数可选，仅LinearSVC有。

　　**loss:**损失函数，有‘hinge’和‘squared_hinge’两种可选，前者又称L1损失，后者称为L2损失，默认是是’squared_hinge’，其中hinge是SVM的标准损失，squared_hinge是hinge的平方

　　**dual:**是否转化为对偶问题求解，默认是True。

　　**tol:**残差收敛条件，默认是0.0001，与LR中的一致。

　　**C:**惩罚系数，用来控制损失函数的惩罚系数，类似于LR中的正则化系数。

　　**multi_class:**负责多分类问题中分类策略制定，有‘ovr’和‘crammer_singer’ 两种参数值可选，默认值是’ovr’，’ovr’的分类原则是将待分类中的某一类当作正类，其他全部归为负类，通过这样求取得到每个类别作为正类时的正确率，取正确率最高的那个类别为正类；‘crammer_singer’ 是直接针对目标函数设置多个参数值，最后进行优化，得到不同类别的参数值大小

　　**fit_intercept:**是否计算截距，与LR模型中的意思一致。

　　**class_weight:**与其他模型中参数含义一样，也是用来处理不平衡样本数据的，可以直接以字典的形式指定不同类别的权重，也可以使用balanced参数值。

　　**verbose:**是否冗余，默认是False。

　　**random_state:**随机种子。

　　**max_iter:**最大迭代次数，默认是1000。

SVM结合TF-IDF原理进行文本分类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
# -*- coding: utf-8 -*-
import jieba
import numpy as np
import os
import time
import codecs
import re
import jieba.posseg as pseg
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
from sklearn.naive_bayes import MultinomialNB
from sklearn.svm import SVC
from sklearn.pipeline import Pipeline
from sklearn import metrics

open=codecs.open
path_en='../After/En'
path_peo='../After/new_people'
content_train_src=[]      #训练集文本列表
opinion_train_stc=[]      #训练集类别列表
file_name_src=[]          #训练集文本文件名列表
train_src=[]              #训练集总列表
test_src=[]               #测试集总列表


def readfile(path):
    for filename in os.listdir(path):
        starttime=time.time()
        filepath=path+"/"+filename
        filestr=open(filepath).read()
        opinion=path[9:]
        train_src.append((filename,filestr,opinion))
        endtime=time.time()
        print '类别:%s >>>>文件:%s >>>>导入用时: %.3f' % (opinion, filename, endtime - starttime)
    return train_src
    
    train_src_all=readfile(path_en)
train_src_all=train_src_all+readfile(path_peo)

def readtrain(train_src_list):
    for (fn,w,s) in train_src_list:
        file_name_src.append(fn)
        content_train_src.append(w)
        opinion_train_stc.append(s)
    train=[content_train_src,opinion_train_stc,file_name_src]
    return train

def segmentWord(cont):
    listseg=[]
    for i in cont:
        Wordp = Word_pseg(i)
        New_str = ''.join(Wordp)
        Wordlist = Word_cut_list(New_str)
        file_string = ''.join(Wordlist)
        listseg.append(file_string)
    return listseg

train=readtrain(train_src_all)
content=segmentWord(train[0])
filenamel=train[2]
opinion=train[1]

train_content=content[:3000]
test_content=content[3000:]
train_opinion=opinion[:3000]
test_opinion=opinion[3000:]
train_filename=filenamel[:3000]
test_filename=filenamel[3000:]

test_all=[test_content,test_opinion,test_filename]


vectorizer=CountVectorizer()
tfidftransformer=TfidfTransformer()
tfidf = tfidftransformer.fit_transform(vectorizer.fit_transform(train_content))  # 先转换成词频矩阵，再计算TFIDF值

print tfidf.shape

word = vectorizer.get_feature_names()
weight = tfidf.toarray()
# 分类器
clf = MultinomialNB().fit(tfidf, opinion)
docs = ["原任第一集团军副军长", "在9·3抗战胜利日阅兵中担任“雁门关伏击战英雄连”英模方队领队记者林韵诗继黄铭少将后"]
new_tfidf = tfidftransformer.transform(vectorizer.transform(docs))
predicted = clf.predict(new_tfidf)
print predicted

# 训练和预测一体
text_clf = Pipeline([('vect', CountVectorizer()), ('tfidf', TfidfTransformer()), ('clf', SVC(C=1, kernel = 'linear'))])
text_clf = text_clf.fit(train_content, train_opinion)
predicted = text_clf.predict(test_content)
print 'SVC',np.mean(predicted == test_opinion)
print set(predicted)
print metrics.confusion_matrix(test_opinion,predicted) # 混淆矩阵

发表于
字数统计: | 阅读时长 ≈

朴素贝叶斯算法

朴素贝叶斯法（Naive Bayes）是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集，首先基于特征条件独立假设学习输入/输出的联合概率分布；然后基于此模型，对给定的输入 xx ，利用贝叶斯定理求出后验概率最大的输出 yy 。

可能读完上面这段话仍旧没办法理解朴素贝叶斯法到底是什么，又是怎样进行分类的。下面我尽可能详细且直观地描述朴素贝叶斯法的工作原理。首先我们需要知道的是，朴素贝叶斯是基于概率论的分类算法。

1. 朴素贝叶斯

朴素贝叶斯被认为是最简单的分类算法之一。首先，我们需要了解一些概率论的基本理论。假设有两个随机变量X和Y，他们分别可以取值为x和y。有这两个随机变量，我们可以定义两种概率：
关键概念：联合概率与条件概率
联合概率：“X取值为x”和“Y取值为y”两个事件同时发生的概率，表示为P(X=x,Y=y)P(X=x,Y=y)      P(X = x, Y = y)P(X=x,Y=y)
条件概率：在X取值为x的前提下，Y取值为y的概率，表示为P(Y=y∣X=x)P(Y=y∣X=x)      P(Y = y | X = x)P(Y=y∣X=x)

在概率论中，我们可以证明，两个事件的联合概率等于这两个事件任意条件概率 * 这个条件事件本身的概率。
P(X=1,Y=1)=P(Y=1∣X=1)∗P(X=1)=P(X=1∣Y=1)∗P(Y=1)P(X=1,Y=1)=P(Y=1∣X=1)∗P(X=1)=P(X=1∣Y=1)∗P(Y=1)      P(X = 1, Y = 1) =P(Y = 1|X = 1)*P(X=1)=P(X = 1|Y=1)*P(Y=1)P(X=1,Y=1)=P(Y=1∣X=1)∗P(X=1)=P(X=1∣Y=1)∗P(Y=1)
简单一些，则可以将上面的式子写成：
P(X,Y)=P(Y∣X)∗P(X)=P(X∣Y)∗P(Y)P(X,Y)=P(Y∣X)∗P(X)=P(X∣Y)∗P(Y)      P(X, Y)=P(Y|X)*P(X)=P(X|Y)*P(Y)P(X,Y)=P(Y∣X)∗P(X)=P(X∣Y)∗P(Y)
由上面的式子，我们可以得到贝叶斯理论等式：
P(Y∣X)=P(X∣Y)∗P(Y)P(X)P(Y∣X)=P(X∣Y)∗P(Y)P(X)      P(Y|X) =  \frac{P(X|Y)*P(Y)}{P(X)}P(Y∣X)=P(X)P(X∣Y)∗P(Y)
而这个式子，就是我们一切贝叶斯算法的根源理论。我们可以把我们的特征XX      XX当成是我们的条件事件，而我们要求解的标签YY      YY当成是我们被满足条件后会被影响的结果，而两者之间的概率关系就是P(Y∣X)P(Y∣X)      P(Y|X)P(Y∣X)，这个概率在机器学习中，被我们称之为是标签的后验概率（posterior probability），即是说我们先知道了条件，再去求解结果。而标签 在没有任何条件限制下取值为某个值的概率，被我们写作P(Y)P(Y)      P(Y)P(Y)，与后验概率相反，这是完全没有任何条件限制的，标签的先验概率（prior probability）。而我们的P(X∣Y)P(X∣Y)      P(X|Y)P(X∣Y) 被称为“类的条件概率”，表示当Y的取值固定的时候，X为某个值的概率。

3.朴素贝叶斯公式的推导

2.贝叶斯估计

3.朴素贝叶斯算法的过程

使用朴素贝叶斯进行文本分类示例

本次使用的数据集来自于业内著名的20 Newsgroups 数据集，包含20类标注好的样本，数据量共计约2万条记录。该数据集每篇文档均不长，即使同时使用多个类目数据合并起来进行建模，在单机上也可快速完成，因此具有很好的学习训练价值。

1
2
3
4
5
6
7
8
9
from time import time
from sklearn.datasets import load_files

#加载数据
print("loading train dataset.....")
t=time()
news_train=load_files('D:/20news/20news-bydate-train/')
print("summary:{0} documents in {1} categories.".format(len(news_train.data),len(news_train.target_names)))
print("done in {0} seconds".format(time()-t))

结果输出:

1
2
3
4
5
6
7
8
9
10
11
12

#将文档转化为TF-IDF形式
from sklearn.feature_extraction.text import TfidfVectorizer

print("vaectoring train dataset......")
t=time()
vectorsize=TfidfVectorizer(encoding="latin-1")
X_train=vectorsize.fit_transform((d for d in news_train.data))#转换为矩阵
print("n_sample:%d,n_features:%d"% X_train.shape)
print("number of non-zero features in sample [{0}]:{1}".format(news_train.filenames[0],X_train[0].getnnz()))#打印
#第一篇文章名称和文章中的词语数
print("done in {0} seconds".format(time()-t))

1
2
3
4
5
6
7
8
9
10
11
12

#使用模块MultinomialNB训练数据集
from sklearn.naive_bayes import MultinomialNB

print("training models....".format(time()-t))
t=time()
y_train=news_train.target#元素大小为0到20的一维矩阵
clf=MultinomialNB(alpha=0.0001)#拼平滑指数，过小容易造成过拟合，过大容易过拟合
clf.fit(X_train,y_train)
train_score=clf.score(X_train,y_train)
print("train_socre :{0}".format(train_score))
print("done in {0} seconds".format(time()-t))

1
2
3
4
5
6
#加载测试集合
print("loading test dataset.....")
t=time()
news_test=load_files("D:/20news/20news-bydate-test/")
print("summary :{0} Documents in {1} catelogies.".format(len(news_test.data),len(news_test.target_names)))
print("done in {0} seconds ".format(time()-t))
1
2
3
4
5
6
7
8
      
      #将测试集向量化
print("向量化测试机集")
y_test=news_test.target
X_test=vectorsize.transform((b for b in news_test.data))
print("n_samples: %d. n_fetures : %d "% X_test.shape)
print("{0} numers of None-zero in file[{1}]".format(X_test[0].getnnz(),news_test.filenames[0]))
print("done in %fs"%(time()-t))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

#取第一篇预测一下
pred=clf.predict(X_test[0])

#print(X_test[0])
print("the first page is {0},the predict is {1}".format(news_test.filenames[0],news_test.target_names[news_test.target[0]]))
#模型评价
#首先对测试机进行预测
print("predicting the test.......")
t0=time()
pred=clf.predict(X_test)
print("done in {0} seconds".format(time()-t0))
#使用classification_report查看每个类别预测的准确性
from sklearn.metrics import classification_report

print("classification_report on test set for classifier:")
print(clf)
print(classification_report(y_test,pred,target_names=news_test.target_names))#精确度，召回率，F1值

print("**********************************************")
#使用confusion_matrix生成混淆矩阵,
from sklearn.metrics import confusion_matrix
cm=confusion_matrix(y_test,pred)
print("confusion_matrix:")
print(cm)

发表于
字数统计: | 阅读时长 ≈

自然语言处理(4):文本表示

1.TF-IDF原理

  1. 词频TF（item frequency）：某一给定词语在该文本中出现次数。该数字通常会被归一化（分子一般小于分母），以防止它偏向长的文件，因为不管该词语重要与否，它在长文件中出现的次数很可能比在段文件中出现的次数更大。 需要注意的是有一些通用词对文章主题没有太大作用，如“的”“是”等，而有一些频率出现少的词如一些专业词更能表现文章主题，所以为词语设置权重，权重的设计满足：一个词预测主题的能力越强，权重越大，反之，权重越小。也就是说，一些词只在很少几篇文章中出现，那么这样的词对文章主题的判断能力很大，这些词的权重应该设计的较大。IDF完成这样的工作。
  2. 逆向文件频率IDF（inverse document frequency）：一个词语普遍重要性的度量。主要思想是：如果包含词条t的文档越少, IDF越大，则说明词条具有很好的类别区分能力。某一特定词语的IDF，可以由总文件数目除以包含该词语之文件的数目，再将得到的商取对数得到。
1
2
TF=(某个词在文章中出现的次数)/(文章的总词数)
IDF=log((语料库的文档总数)/(包含该词的文档数+1))

2.使用不同的方法来计算TF-IDF的值

  1. 词袋模型
    Bag of words，也叫做“词袋”，在信息检索中，Bag of words model假定对于一个文本，忽略其词序和语法，句法，将其仅仅看做是一个词集合，或者说是词的一个组合，文本中每个词的出现都是独立的，不依赖于其他词是否出现，或者说当这篇文章的作者在任意一个位置选择一个词汇都不受前面句子的影响而独立选择的。
1.使用gensim模块
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
corpus = [
    'this is the first document',
    'this is the second second document',
    'and the third one',
    'is this the first document'
]#语料库

#先做分词处理
word_list=[]
for i in range(len(corpus)):
    word_list.append(corpus[i].split(' '))
print(word_list)

#得到每个词的id值和词频

from gensim import corpora
dic=corpora.Dictionary(word_list)#赋给语料库中每个不重复的词一个id
new_corpus=[dic.doc2bow(text) for text in word_list]#寻找整篇语料的词典、所有词，corpora.Dictionary
print(new_corpus)

#训练gensim模型
from gensim import models
tfidf=models.TfidfModel(new_corpus)
tfidf.save("my_model.tfidf")

#载入模型
tfidf=models.TfidfModel.load("my_model.tfidf")
#使用模型得到单词的tfidf值
tfidf_vec=[]
for i in range(len(corpus)):
    string=corpus[i]
    string_bow=dic.doc2bow(string.lower().split())
    stringtfidf=tfidf[string_bow]
    tfidf_vec.append(stringtfidf)
print(tfidf_vec)
  1. 结论
  • gensim训练出来的tf-idf值左边是词的id，右边是词的tfidf值
  • gensim有自动去除停用词的功能，比如the
  • gensim会自动去除单个字母，比如i
  • gensim会去除没有被训练到的词，比如name
    所以通过gensim并不能计算每个单词的tfidf值
2.使用sklearn提取文本tfidf特征
1
2
3
4
5
6
7
from sklearn.feature_extraction.text import TfidfVectorizer
tfidf_vec=TfidfVectorizer()#模型构建
tfidf_matrix=tfidf_vec.fit_transform(corpus)#传入句子组成的list

print(tfidf_vec.get_feature_names())#得到所有不重复的词
print(tfidf_vec.vocabulary_)#得到对应的id值
print(tfidf_matrix.toarray())
3.python提取文本特征tfidf值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#统计词频
from collections import Counter
countlist=[]
for i in range(len(word_list)):
    count=Counter(word_list[i])#每个count是一个句子
    countlist.append(count)
# word可以通过count得到，count可以通过countlist得到
# count[word]可以得到每个单词的词频， sum(count.values())得到整个句子的单词总数
def tf(word,count):
    return count[word]/sum(count.values())
#统计含有该单词的句子数
def n_containing(word,countlist):
    return sum(1 for count in countlist if word in count)
# len(count_list)是指句子的总数，n_containing(word, count_list)是指含有该单词的句子的总数，加1是为了防止分母为0
def idf(word, count_list):
    return math.log(len(count_list) / (1 + n_containing(word, count_list)))

# 将tf和idf相乘
def tfidf(word, count, count_list):
    return tf(word, count) * idf(word, count_list)

import math
for i,count in enumerate(countlist):
    print("Top words in docment{}".format(i+1))
    scores={word:tfidf(word,count,countlist) for word in count}
    sorted_words=sorted(scores.items(),key=lambda x:x[1],reverse=True)
    for word,score in sorted_words[:]:
        print("\tWord: {}, TF-IDF: {}".format(word, round(score, 5)))

3.sklearn：点互信息和互信息

  1. 点互信息PMI
    机器学习相关文献里面，经常会用到点互信息PMI(Pointwise Mutual Information)这个指标来衡量两个事物之间的相关性（比如两个词）。
    在概率论中，我们知道，如果x跟y不相关，则p(x,y)=p(x)p(y)。二者相关性越大，则p(x, y)就相比于p(x)p(y)越大。用后面的式子可能更好理解，在y出现的情况下x出现的条件概率p(x|y)除以x本身出现的概率p(x)，自然就表示x跟y的相关程度。举个自然语言处理中的例子来说，我们想衡量like这个词的极性（正向情感还是负向情感）。我们可以预先挑选一些正向情感的词，比如good。然后我们算like跟good的PMI。
1
PMI(x;y)=log(p(x,y)/(p(x)*p(y)))=log(p(y|x)/p(y))
  1. 互信息MI
    衡量的是两个随机变量之间的相关性，即一个随机变量中包含的关于另一个随机变量的信息量。所谓的随机变量，即随机试验结果的量的表示，可以简单理解为按照一个概率分布进行取值的变量，比如随机抽查的一个人的身高就是一个随机变量。可以看出，互信息其实就是对X和Y的所有可能的取值情况的点互信息PMI的加权和。因此，点互信息这个名字还是很形象的。

4.如何进行特征选择（理论篇）机器学习你会遇到的“坑”(来源于网络)

一个典型的机器学习任务，是通过样本的特征来预测样本所对应的值。如果样本的特征少了，我们会考虑增加特征，比如Polynomial Regression就是典型的增加特征的算法。在前一周的课程中，相信大家已经体会到，模型特征越多，模型的复杂度也就越高，越容易导致过拟合。事实上，如果我们的样本数少于特征数，那么过拟合就不可避免。

而现实中的情况，往往是特征太多了，需要减少一些特征。

首先是“无关特征”（irrelevant feature）。比如，通过空气的湿度，环境的温度，风力和当地人的男女比例来预测明天会不会下雨，其中男女比例就是典型的无关特征。

其次，要减少的另一类特征叫做“多余特征”（redundant feature），比如，通过房屋的面积，卧室的面积，车库的面积，所在城市的消费水平，所在城市的税收水平等特征来预测房价，那么消费水平（或税收水平）就是多余特征。证据表明，消费水平和税收水平存在相关性，我们只需要其中一个特征就够了，因为另一个能从其中一个推演出来。（如果是线性相关，那么我们在用线性模型做回归的时候，会出现严重的多重共线性问题，将会导致过拟合。）

减少特征有非常重要的现实意义，甚至有人说，这是工业界最重要的问题。因为除了降低过拟合，特征选择还可以使模型获得更好的解释性，加快模型的训练速度，一般的，还会获得更好的性能。

问题在于，在面对未知领域的时候，很难有足够的知识去判断特征与我们的目标是不是相关，特征与特征之间是不是相关。这时候，就需要一些数学和工程上的办法来帮助我们尽可能地把恰好需要的特征选择出来。

常见的方法包括过滤法（Filter）、包裹法（Warpper），嵌入法

1.过滤法

过滤法只用于检验特征向量和目标（响应变量）的相关度，不需要任何的机器学习的算法，不依赖于任何模型，只是应用统计量做筛选：我们根据统计量的大小，设置合适的阈值，将低于阈值的特征剔除.

2.包裹法

与过滤法不同的是，包裹法采用的是特征搜索的办法。它的基本思路是，从初始特征集合中不断的选择子集合，根据学习器的性能来对子集进行评价，直到选择出最佳的子集。在搜索过程中，我们会对每个子集做建模和训练。

图为包裹法的流程图，其中Estimated Accuracy是机器学习分类问题的典型的性能指标。

基于此，包裹法很大程度上变成了一个计算机问题：在特征子集的搜索问题（subset search）。我们有多种思路，最容易想到的办法是穷举（Brute-force search），遍历所有可能的子集，但这样的方法适用于特征数较少的情形，特征一旦增多，就会遇到组合爆炸，在计算上并不可行。（N个特征，则子集会有种可能）

另一个思路是随机化搜索，比如拉斯维加斯算法（Las Vegas algorithm），但这样的算法在特征数大的时候，计算开销仍然很大，而且有给不出任何解的风险。所以，我们常使用的是贪心算法：

  • 前向搜索（Forward search）

在开始时，按照特征数来划分子集，每个子集只有一个特征，对每个子集进行评价。然后在最优的子集上逐步增加特征，使模型性能提升最大，直到增加特征并不能使模型性能提升为止。

  • 后向搜索（Backward search）

在开始时，将特征集合分别减去一个特征作为子集，每个子集有N—1个特征，对每个子集进行评价。然后在最优的子集上逐步减少特征，使得模型性能提升最大，直到减少特征并不能使模型性能提升为止。

  • 双向搜索（Bidirectional search）

将Forward search 和Backward search结合起来。

  • 递归剔除（Recursive elimination ）

反复的训练模型，并剔除每次的最优或者最差的特征，将剔除完毕的特征集进入下一轮训练，直到所有的特征被剔除，被剔除的顺序度量了特征的重要程度。

发表于
字数统计: | 阅读时长 ≈

NPL之基本文本处理技能

1.分词的概念

一个良好的分词系统应由词典和统计两套系统组成。后者为前者构造可持续更新的词典，识别新词，同时对消岐部分进行匹配。在分词过程中，好的词典很重要，其次算法要跟着需求走，不同需求选择不同算法，比如有些要求速度快，与兴趣相关，此时算法是次要的，而有些需求注重的是精度。

现有方法：基于词典的匹配：前向最大匹配，后向最大匹配；基于字的标注：最大熵模型，条件随机场模型，感知器模型；其他方法：与词性标注集合，与句法分析结合。

2.分词最大向量化，逆向最大，双向最大匹配法

1.分词最大正向匹配法（示例来自网络）

1、正向最大匹配法：
正向即从前往后取词，从7->1，每次减一个字，直到词典命中或剩下1个单字。
第1次：“我们在野生动物”，扫描7字词典，无
第2次：“我们在野生动”，扫描6字词典，无
。。。。
第6次：“我们”，扫描2字词典，有
扫描中止，输出第1个词为“我们”，去除第1个词后开始第2轮扫描，即：
第2轮扫描：
第1次：“在野生动物园玩”，扫描7字词典，无
第2次：“在野生动物园”，扫描6字词典，无
。。。。
第6次：“在野”，扫描2字词典，有
扫描中止，输出第2个词为“在野”，去除第2个词后开始第3轮扫描，即：
第3轮扫描：
第1次：“生动物园玩”，扫描5字词典，无
第2次：“生动物园”，扫描4字词典，无
第3次：“生动物”，扫描3字词典，无
第4次：“生动”，扫描2字词典，有
扫描中止，输出第3个词为“生动”，第4轮扫描，即：
第4轮扫描：
第1次：“物园玩”，扫描3字词典，无
第2次：“物园”，扫描2字词典，无
第3次：“物”，扫描1字词典，无
扫描中止，输出第4个词为“物”，非字典词数加1，开始第5轮扫描，即：
第5轮扫描：
第1次：“园玩”，扫描2字词典，无
第2次：“园”，扫描1字词典，有
扫描中止，输出第5个词为“园”，单字字典词数加1，开始第6轮扫描，即：
第6轮扫描：
第1次：“玩”，扫描1字字典词，有
扫描中止，输出第6个词为“玩”，单字字典词数加1，整体扫描结束。
正向最大匹配法，最终切分结果为：“我们/在野/生动/物/园/玩”，其中，单字字典词为2，非词典词为1。

2.逆向最大匹配法

逆向即从后往前取词，其他逻辑和正向相同。即：
第1轮扫描：“在野生动物园玩”
第1次：“在野生动物园玩”，扫描7字词典，无
第2次：“野生动物园玩”，扫描6字词典，无
。。。。
第7次：“玩”，扫描1字词典，有
扫描中止，输出“玩”，单字字典词加1，开始第2轮扫描
第2轮扫描：“们在野生动物园”
第1次：“们在野生动物园”，扫描7字词典，无
第2次：“在野生动物园”，扫描6字词典，无
第3次：“野生动物园”，扫描5字词典，有
扫描中止，输出“野生动物园”，开始第3轮扫描
第3轮扫描：“我们在”
第1次：“我们在”，扫描3字词典，无
第2次：“们在”，扫描2字词典，无
第3次：“在”，扫描1字词典，有
扫描中止，输出“在”，单字字典词加1，开始第4轮扫描
第4轮扫描：“我们”
第1次：“我们”，扫描2字词典，有
扫描中止，输出“我们”，整体扫描结束。
逆向最大匹配法，最终切分结果为：“我们/在/野生动物园/玩”，其中，单字字典词为2，非词典词为0。

3.双向最大匹配法

正向最大匹配法和逆向最大匹配法，都有其局限性(如：长春药店，逆向切分为“长/春药店”），因此有人又提出了双向最大匹配法，双向最大匹配法。即，两种算法都切一遍，然后根据大颗粒度词越多越好，非词典词和单字词越少越好的原则，选取其中一种分词结果输出。
如：“我们在野生动物园玩”
正向最大匹配法，最终切分结果为：“我们/在野/生动/物/园/玩”，其中，两字词3个，单字字典词为2，非词典词为1。
逆向最大匹配法，最终切分结果为：“我们/在/野生动物园/玩”，其中，五字词1个，两字词1个，单字字典词为2，非词典词为0。
非字典词：正向(1)>逆向(0)（越少越好）
单字字典词：正向(2)=逆向(2)（越少越好）
总词数：正向(6)>逆向(4)（越少越好）
因此最终输出为逆向结果。

2.Python标准库——collections模块的Counter类

Counter类的目的是用来跟踪值出现的次数。它是一个无序的容器类型，以字典的键值对形式存储，其中元素作为key，其计数作为value。计数值可以是任意的Interger（包括0和负数）

1.创建
1
2
3
4
>>> c = Counter()  # 创建一个空的Counter类
>>> c = Counter('gallahad')  # 从一个可iterable对象（list、tuple、dict、字符串等）创建
>>> c = Counter({'a': 4, 'b': 2})  # 从一个字典对象创建
>>> c = Counter(a=4, b=2)  # 从一组键值对创建
2.2 计数值的访问与缺失的键

当所访问的键不存在时，返回0，而不是KeyError；否则返回它的计数。

1
2
3
4
5
6
7
>>> c = Counter("abcdefgab")
>>> c["a"]
2
>>> c["c"]
1
>>> c["h"]
0
3. 计数器的更新（update和subtract）

可以使用一个iterable对象或者另一个Counter对象来更新键值。
计数器的更新包括增加和减少两种。其中，增加使用update()方法：

1
2
3
4
5
6
7
8
>>> c = Counter('which')
>>> c.update('witch')  # 使用另一个iterable对象更新
>>> c['h']
3
>>> d = Counter('watch')
>>> c.update(d)  # 使用另一个Counter对象更新
>>> c['h']
4
4.元素的删除

删除元素使用del

5 elements()

返回一个迭代器。元素被重复了多少次，在该迭代器中就包含多少个该元素。元素排列无确定顺序，个数小于1的元素不被包含。

1
2
3
>>> c = Counter(a=4, b=2, c=0, d=-2)
>>> list(c.elements())
['a', 'a', 'a', 'a', 'b', 'b']
6.most_common([n])

返回一个TopN列表。如果n没有被指定，则返回所有元素。当多个元素计数值相同时，排列是无确定顺序的。

1
2
3
4
5
>>> c = Counter('abracadabra')
>>> c.most_common()
[('a', 5), ('r', 2), ('b', 2), ('c', 1), ('d', 1)]
>>> c.most_common(3)
[('a', 5), ('r', 2), ('b', 2)]
7.常规操作
1
2
3
4
5
6
7
8
9
sum(c.values())  # 所有计数的总数
c.clear()  # 重置Counter对象，注意不是删除
list(c)  # 将c中的键转为列表
set(c)  # 将c中的键转为set
dict(c)  # 将c中的键值对转为字典
c.items()  # 转为(elem, cnt)格式的列表
Counter(dict(list_of_pairs))  # 从(elem, cnt)格式的列表转换为Counter类对象
c.most_common()[:-n:-1]  # 取出计数最少的n-1个元素
c += Counter()  # 移除0和负值

3.语言模型中unigram、bigram、trigram的概念

  1. unigram 一元分词，把句子分成一个一个的汉字
  2. bigram 二元分词，把句子从头到尾每两个字组成一个词语
  3. trigram 三元分词，把句子从头到尾每三个字组成一个词语.
n-gram模型的概念

n-gram模型也称为n-1阶马尔科夫模型，它有一个有限历史假设：当前词的出现概率仅仅与前面n-1个词相关。因此(1)式可以近似为：

当n取1、2、3时，n-gram模型分别称为unigram、bigram和trigram语言模型。n-gram模型的参数就是条件概率

假设词表的大小为100,000，那么n-gram模型的参数数量为

n越大，模型越准确，也越复杂，需要的计算量越大。最常用的是bigram，其次是unigram和trigram，n取≥4的情况较少。

4.文本矩阵化(要求采用结巴分词来进行分词操作)

分词（可采用结巴分词来进行分词操作，其他库也可以）；去停用词；构造词表。
每篇文档的向量化。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import jieba
import re
stopwords = {}
fstop = open('stop_words.txt', 'r',encoding='utf-8',errors='ingnore')
for eachWord in fstop:
    stopwords[eachWord.strip()] = eachWord.strip()  #停用词典
fstop.close()
f1=open('tt1.txt','r',encoding='utf-8',errors='ignore')
f2=open('fenci.txt','w',encoding='utf-8')

line=f1.readline()
while line:
    line = line.strip()  #去前后的空格
    line = re.sub(r"[0-9\s+\.\!\/_,$%^*()?;；:-【】+\"\']+|[+——！，;:。？、~@#￥%……&*（）]+", " ", line) #去标点符号
    seg_list=jieba.cut(line,cut_all=False)  #结巴分词
    outStr=""
    for word in seg_list:
        if word not in stopwords:
            outStr+=word
            outStr+=" "
    f2.write(outStr)
    line=f1.readline()
f1.close()
f2.close()

#####