神经网络基础

1.RNN结构

(1).背景

DNN以及CNN在对样本提取特征的时候，样本与样本之间是独立的，而有些情况是无法把每个输入的样本都看作是独立的，比如NLP中的此行标注问题，ASR中每个音素都和前一个音素是相关的，这类问题可以看做一种带有时序序列的问题，无法将样本看做是相互独立的，因此单纯的DNN和CNN解决这类问题就比较棘手。此时RNN就是一种解决这类问题很好的模型。

特点：

权重W,U,V是共享的，以此减少参数量
第t时刻的输出与第t-1时刻的输出有关

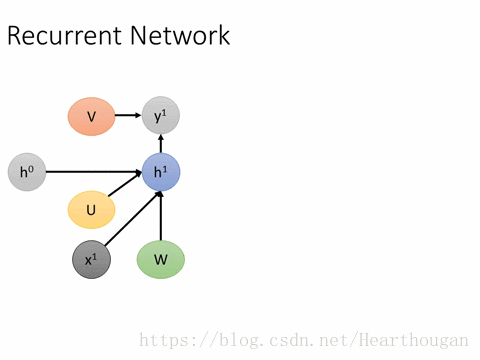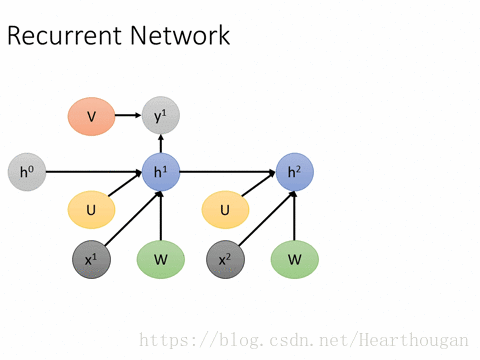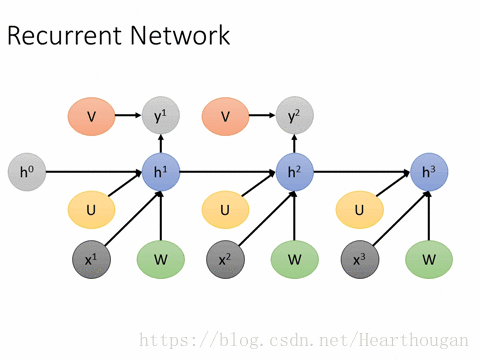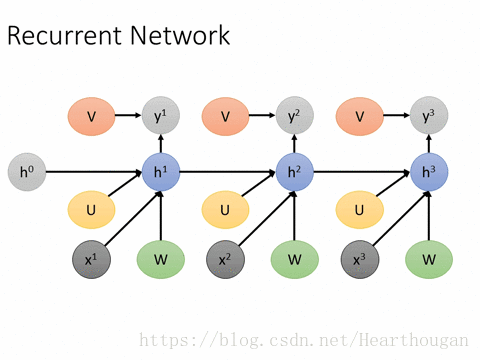
(2).优缺点，存在的问题

DNN无法对时间序列上有变化的情况进行处理。然而，样本出现的时间顺序对于自然语言处理、语音识别、手写体识别等应用非常重要。因此出现了——循环神经网络RNN。
在普通的全连接网络或CNN中，每层神经元的信号只能向上一层传播，样本的处理在各个时刻独立，因此又被成为前向神经网络(Feed-forward Neural Networks)。而在RNN中，神经元的输出可以在下一个时间段直接作用到自身，即第i层神经元在m时刻的输入，除了(i-1)层神经元在该时刻的输出外，还包括其自身在(m-1)时刻的输出！

但是出现了一个问题——“梯度消失”现象又要出现了，只不过这次发生在时间轴上。
所以RNN存在无法解决长时依赖的问题。为解决上述问题，提出了LSTM（长短时记忆单元），通过cell门开关实现时间上的记忆功能，并防止梯度消失.

(3).RNN如何实现参数更新(基于时间得反向传播算法 BPTT)

下图展示了在训练过程中的损失的产生：

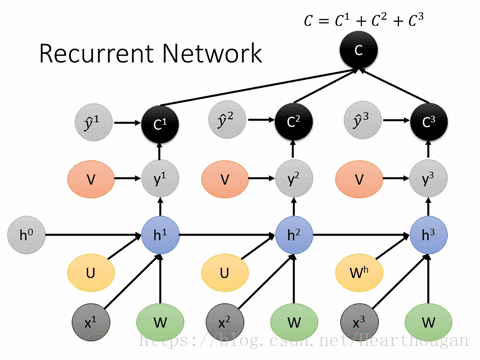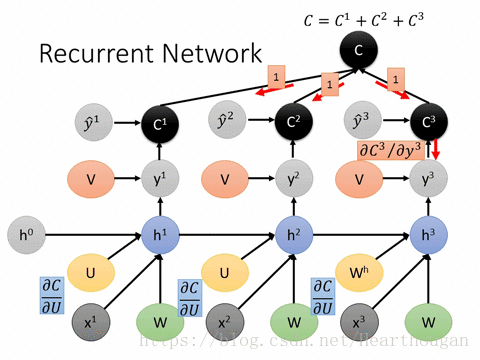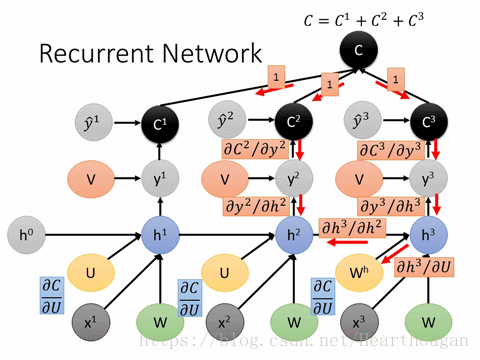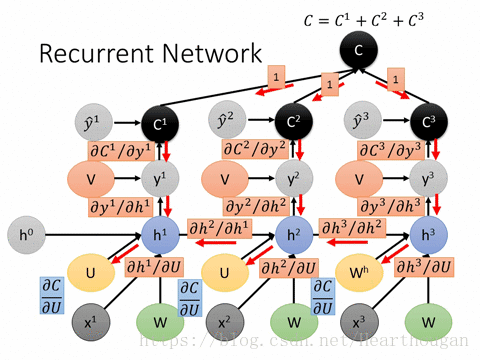
详细的数学推导过程：

首先列出在推导过程中的一般计算公式：

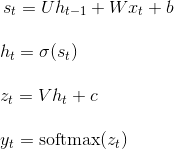
将输出对应的损失求导：

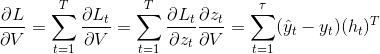
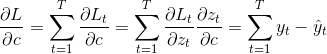
接下来是对参数W,U,b进行更新，虽然三者在过程中是共享的，但是他们不止在t时刻做出了贡献，在t+1时刻也对隐藏层St+1做出了贡献，所以求导时，要从前往后一步步推导。

三者有一个共同项，所以先求这个共同项：

在求解激活函数导数时，是将已知的部分求导之后，然后将它和激活函数导数部分进行哈达马乘积。激活函数的导数一般是和前面的进行哈达马乘积，这里的激活函数是双曲正切，用矩阵中对角线元素表示向量中各个值的导数，可以去掉哈达马乘积，转化为矩阵乘法。

在求得了st以后，将其带回最初得公式对参数进行求导：

在有了各个导数以后，对参数进行更新：

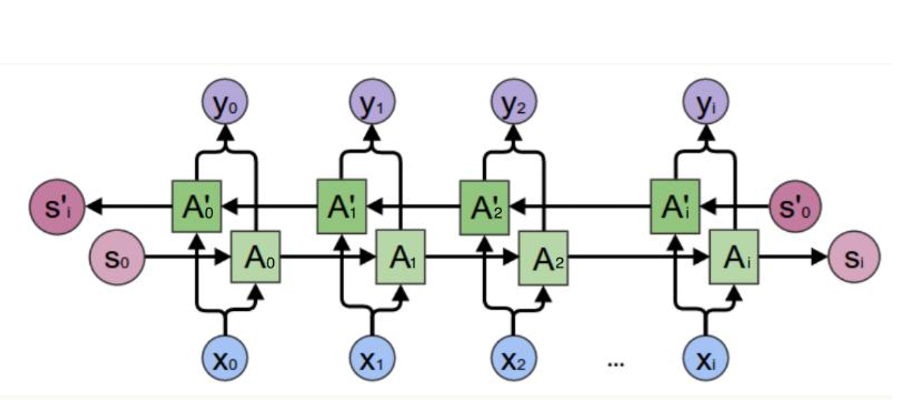
2.双向RNN

Bidirectional RNN(双向RNN)假设当前t的输出不仅仅和之前的序列有关，并且还与之后的序列有关，例如：预测一个语句中缺失的词语那么需要根据上下文进行预测；Bidirectional RNN是一个相对简单的RNNs，由两个RNNs上下叠加在一起组成。输出由这两个RNNs的隐藏层的状态决定。

3.LSTM

LSTM 通过刻意的设计来避免长期依赖问题。记住长期的信息在实践中是 LSTM 的默认行为，

4.Text-RNN原理

TextCNN擅长捕获更短的序列信息，但是TextRNN擅长捕获更长的序列信息。

代码实现

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
tf.set_random_seed(1)

mnist = input_data.read_data_sets('MNIST_data', one_hot=True)

# hyperparameters
lr = 0.001
training_iters = 100000
batch_size = 128

n_inputs = 28  # shape 28*28
n_steps = 28  # time steps
n_hidden_unis = 128  # neurons in hidden layer
n_classes = 10  # classes 0-9

# tf Graph input
x = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.float32, [None, n_classes])

# Define weights
weights = {
    # (28,128)
    'in': tf.Variable(tf.random_normal([n_inputs, n_hidden_unis])),
    # (128,10)
    'out': tf.Variable(tf.random_normal([n_hidden_unis, n_classes]))
}
biases = {
    # (128,)
    'in': tf.Variable(tf.constant(0.1, shape=[n_hidden_unis, ])),
    # (10,)
    'out': tf.Variable(tf.constant(0.1, shape=[n_classes, ]))
}


def RNN(X, weights, biases):

    # hidden layer for input to cell
    # X(128 batch, 28 steps, 28 inputs) => (128*28, 28)
    X = tf.reshape(X, [-1, n_inputs])
    # ==>(128 batch * 28 steps, 28 hidden)
    X_in = tf.matmul(X, weights['in'])+biases['in']
    # ==>(128 batch , 28 steps, 28 hidden)
    X_in = tf.reshape(X_in,[-1, n_steps, n_hidden_unis])


    # cell
    lstm_cell = tf.contrib.rnn.BasicLSTMCell(n_hidden_unis, forget_bias=1.0, state_is_tuple=True)
    # lstm cell is divided into two parts(c_state, m_state)
    _init_state = lstm_cell.zero_state(batch_size, dtype=tf.float32)
    outputs, states = tf.nn.dynamic_rnn(lstm_cell, X_in, initial_state=_init_state, time_major=False)


    # hidden layer for output as the final results
    results = tf.matmul(states[1], weights['out']) + biases['out']  # states[1]->m_state states[1]=output[-1]
    # outputs = tf.unstack(tf.transpose(outputs,[1,0,2]))
    # results = tf.matmul(outputs[-1], weights['out']) + biases['out']
    return results


pred = RNN(x, weights, biases)
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=pred, labels=y))
train_op = tf.train.AdamOptimizer(lr).minimize(cost)

correct_pred = tf.equal(tf.argmax(pred, 1), tf.argmax(y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

init = tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)
    step = 0
    while step * batch_size < training_iters:
        batch_xs, batch_ys = mnist.train.next_batch(batch_size)
        batch_xs = batch_xs.reshape([batch_size, n_steps, n_inputs])
        sess.run([train_op], feed_dict={
            x: batch_xs,
            y: batch_ys
        })
        if step % 20 ==0:
            print (sess.run(accuracy, feed_dict={
            x: batch_xs,
            y: batch_ys
        }))
        step += 1