汇总:常见算法图示(转自网络)
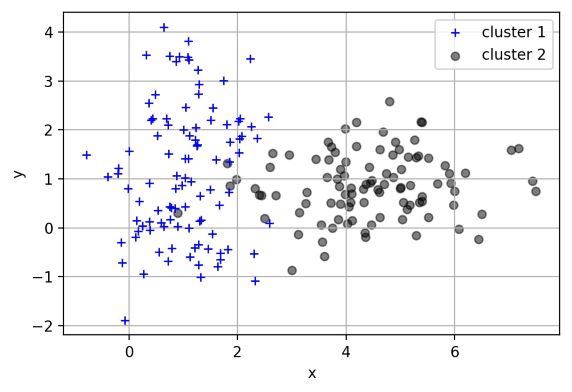
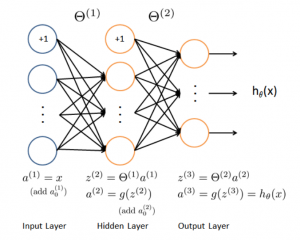
日常使用机器学习的任务中,我们经常会遇见各种算法,下图是各种常见算法的图示。
| 回归算法 | 聚类算法 | 正则化方法 |
|---|---|---|
 |
 |
 |
| 决策树学习 | 贝叶斯方法 | 基于核的算法 |
|---|---|---|
 |
 |
 |
| 聚类算法 | 关联规则学习 | 人工神经网络 |
|---|---|---|
 |
 |
 |
| 深度学习 | 降低维度算法 | 集成算法 |
|---|---|---|
 |
 |
 |
图 1各种常见算法图示
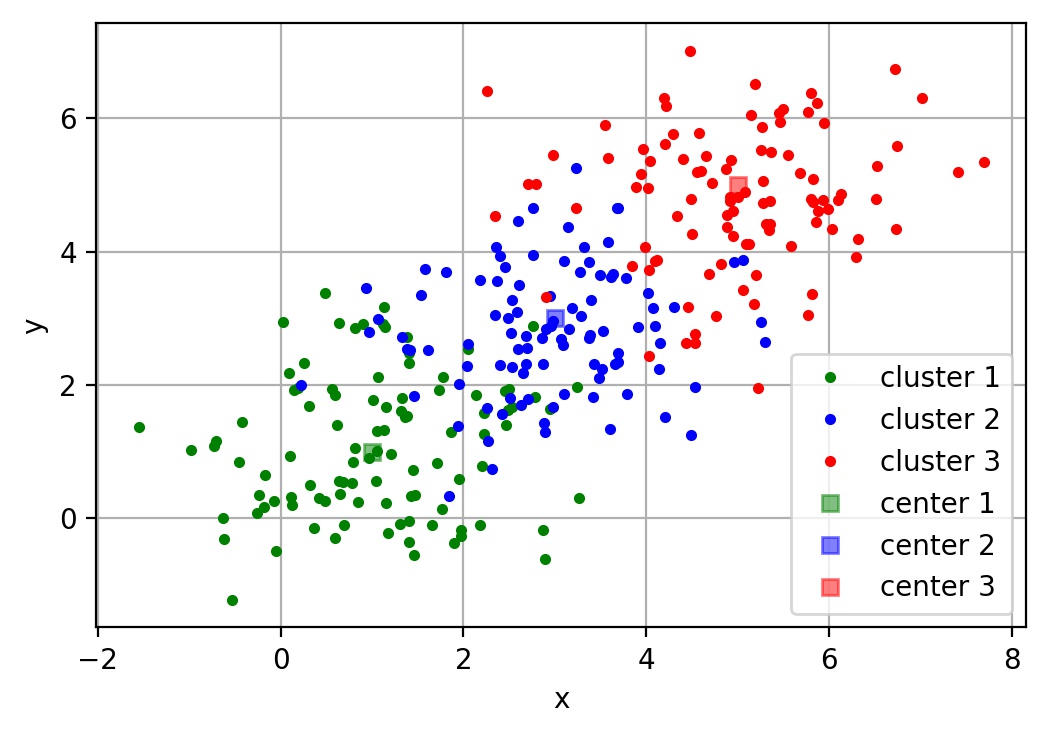
聚类用于找寻数据内在的分布结构,既可以作为一个单独的过程,比如异常检测等等。也可作为分类等其他学习任务的前驱过程。聚类是标准的无监督学习。
1)在一些推荐系统中需确定新用户的类型,但定义“用户类型”却可能不太容易,此时往往可先对原有的用户数据进行聚类,根据聚类结果将每个簇定义为一个类,然后再基于这些类训练分类模型,用于判别新用户的类型。
2)而降维则是为了缓解维数灾难的一个重要方法,就是通过某种数学变换将原始高维属性空间转变为一个低维“子空间”。其基于的假设就是,虽然人们平时观测到的数据样本虽然是高维的,但是实际上真正与学习任务相关的是个低维度的分布。从而通过最主要的几个特征维度就可以实现对数据的描述,对于后续的分类很有帮助。比如对于Kaggle上的泰坦尼克号生还预测问题。通过给定一个乘客的许多特征如年龄、姓名、性别、票价等,来判断其是否能在海难中生还。这就需要首先进行特征筛选,从而能够找出主要的特征,让学习到的模型有更好的泛化性。
聚类和降维都可以作为分类等问题的预处理步骤。
但是他们虽然都能实现对数据的约减。但是二者适用的对象不同,聚类针对的是数据点,而降维则是对于数据的特征。另外它们有着很多种实现方法。聚类中常用的有K-means、层次聚类、基于密度的聚类等;降维中常用的则PCA、Isomap、LLE等。
不同聚类算法有不同的优劣和不同的适用条件。可从以下方面进行衡量判断:
1、算法的处理能力:处理大的数据集的能力,即算法复杂度;处理数据噪声的能力;处理任意形状,包括有间隙的嵌套的数据的能力;
2、算法是否需要预设条件:是否需要预先知道聚类个数,是否需要用户给出领域知识;
3、算法的数据输入属性:算法处理的结果与数据输入的顺序是否相关,也就是说算法是否独立于数据输入顺序;算法处理有很多属性数据的能力,也就是对数据维数是否敏感,对数据的类型有无要求。
聚类(Clustering)
聚类,简单地说就是把相似的东西分到一组,聚类的时候,我们并不关心某一类是什么,我们需要实现的目标只是把相似的东西聚到一起。一个聚类算法通常只需要知道如何计算相似度就可以开始工作了,因此聚类通常并不需要使用训练数据进行学习,在机器学习中属于无监督学习。
分类(Classification)
分类,对于一个分类器,通常需要标注号的数据集。一般情况下,一个分类器会从它得到的训练集中进行学习,从而具备对未知数据进行分类的能力,在机器学习中属于监督学习。
聚类就是按照某个特定标准把一个数据集分割成不同的类或簇,使得同一个簇内的数据对象的相似性尽可能大,同时不在同一个簇中的数据对象的差异性也尽可能地大。即聚类后同一类的数据尽可能聚集到一起,不同类数据尽量分离。
主要的聚类算法可以划分为如下几类:划分方法、层次方法、基于密度的方法、基于网格的方法以及基于模型的方法。
k-means是划分方法中较经典的聚类算法之一。由于该算法的效率高,所以在对大规模数据进行聚类时被广泛应用。k-means算法以k为参数,把n个对象分成k个簇,使簇内具有较高的相似度,而簇间的相似度较低。k-means算法的处理过程如下:首先,随机地 选择k个对象,每个对象初始地代表了一个簇的平均值或中心;对剩余的每个对象,根据其与各簇中心的距离,将它赋给最近的簇;然后重新计算每个簇的平均值。 这个过程不断重复,直到准则函数收敛。通常,采用平方误差准则,其定义如下:
这里E是数据中所有对象的平方误差的总和,p是空间中的点,$m_i$是簇$C_i$的平均值[9]。该目标函数使生成的簇尽可能紧凑独立,使用的距离度量是欧几里得距离,当然也可以用其他距离度量。
算法流程:
(1) 任意选择k个对象作为初始的簇中心;
(2) 根据簇中对象的平均值,将每个对象(重新)赋予最类似的簇;
(3) 更新簇的平均值,即计算每个簇中对象的平均值;
(4) 重复步骤(2)、(3)直到簇中心不再变化;
根据层次分解的顺序是自底向上的还是自上向下的,层次聚类算法分为凝聚的层次聚类算法和分裂的层次聚类算法。
凝聚型层次聚类的策略是先将每个对象作为一个簇,然后合并这些原子簇为越来越大的簇,直到所有对象都在一个簇中,或者某个终结条件被满足。绝大多数层次聚类属于凝聚型层次聚类,它们只是在簇间相似度的定义上有所不同。
算法流程:
注:以采用最小距离的凝聚层次聚类算法为例:
(1) 将每个对象看作一类,计算两两之间的最小距离;
(2) 将距离最小的两个类合并成一个新类;
(3) 重新计算新类与所有类之间的距离;
(4) 重复(2)、(3),直到所有类最后合并成一类。
该算法假设在输入对象中存在一些拓扑结构或顺序,可以实现从输入空间(n维)到输出平面(2维)的降维映射,其映射具有拓扑特征保持性质,与实际的大脑处理有很强的理论联系。
SOM网络包含输入层和输出层。输入层对应一个高维的输入向量,输出层由一系列组织在2维网格上的有序节点构成,输入节点与输出节点通过权重向量连接。 学习过程中,找到与之距离最短的输出层单元,即获胜单元,对其更新。同时,将邻近区域的权值更新,使输出节点保持输入向量的拓扑特征。
算法流程:
(1) 网络初始化,对输出层每个节点权重赋初值;
(2) 从输入样本中随机选取输入向量并且归一化,找到与输入向量距离最小的权重向量;
(3) 定义获胜单元,在获胜单元的邻近区域调整权重使其向输入向量靠拢;
(4) 提供新样本、进行训练;
(5) 收缩邻域半径、减小学习率、重复,直到小于允许值,输出聚类结果。
FCM算法是一种以隶属度来确定每个数据点属于某个聚类程度的算法。
设数据集X={x_1,x_2,…,x_n},它的模糊c划分可用模糊矩阵U=[u_(ij) ]表示,矩阵U的元素u_(ij)表示第j(j=1,2,…,n)个数据点属于第i(i=1,2,…,c)类的隶属度,u_(ij)满足如下条件:
目前被广泛使用的聚类准则是取类内加权误差平方和的极小值。即:
其中V为聚类中心,m为加权指数,d_{ij}(x_j,v_i)=||v_i - x_j||。
算法流程:
(1) 标准化数据矩阵;
(2) 建立模糊相似矩阵,初始化隶属矩阵;
(3) 算法开始迭代,直到目标函数收敛到极小值;
(4) 根据迭代结果,由最后的隶属矩阵确定数据所属的类,显示最后的聚类结果。
假如数据集包含10张照片,照片中包含三角形和圆两种形状。现在来设计一个分类器进行训练,让这个分类器对其他的照片进行正确分类(假设三角形和圆的总数是无限大),简单的,我们用一个特征进行分类:
图a
从上图可看到,如果仅仅只有一个特征进行分类,三角形和圆几乎是均匀分布在这条线段上,很难将10张照片线性分类。那么,增加一个特征后的情况会怎么样:
图b
增加一个特征后,我们发现仍然无法找到一条直线将三角形和圆形分开。所以,考虑需要再增加一个特征:
图c
图d
此时,可以找到一个平面将三角形和圆分开。
计算不同特征数是样本的密度:
(1)一个特征时,假设特征空间时长度为5的线段,则样本密度为10/5 = 2。
(2)两个特征时,特征空间大小为5 * 5 = 25,样本密度为10/25 = 0.4。
(3)三个特征时,特征空间大小是5 5 5 = 125,样本密度为10 / 125 = 0.08。
以此类推,如果继续增加特征数量,样本密度会越来越稀疏,此时,更容易找到一个超平面将训练样本分开。当特征数量增长至无限大时,样本密度就变得非常稀疏。
图e
上图是将三维特征空间映射到二维特征空间后的结果。尽管在高维特征空间时训练样本线性可分,但是映射到低维空间后,结果正好相反。事实上,增加特征数量使得高维空间线性可分,相当于在低维空间内训练一个复杂的非线性分类器。不过,这个非线性分类器太过“聪明”,仅仅学到了一些特例。如果将其用来辨别那些未曾出现在训练样本中的测试样本时,通常结果不太理想,会造成过拟合问题。
图f
上图所示的只采用2个特征的线性分类器分错了一些训练样本,准确率似乎没有图e的高,但是,采用2个特征的线性分类器的泛化能力比采用3个特征的线性分类器要强。因为,采用2个特征的线性分类器学习到的不只是特例,而是一个整体趋势,对于那些未曾出现过的样本也可以比较好地辨别开来。换句话说,通过减少特征数量,可以避免出现过拟合问题,从而避免“维数灾难”。
假设只有一个特征时,特征的值域是0到1,每一个三角形和圆的特征值都是唯一的。如果我们希望训练样本覆盖特征值值域的20%,那么就需要三角形和圆总数的20%。我们增加一个特征后,为了继续覆盖特征值值域的20%就需要三角形和圆总数的45%(0.452的平方约等于0.2)。继续增加一个特征后,需要三角形和圆总数的58%(0.583的三次方约等于0.2)。随着特征数量的增加,为了覆盖特征值值域的20%,就需要更多的训练样本。如果没有足够的训练样本,就可能会出现过拟合问题。
通过上述例子,我们可以看到特征数量越多,训练样本就会越稀疏,分类器的参数估计就会越不准确,更加容易出现过拟合问题。“维数灾难”的另一个影响是训练样本的稀疏性并不是均匀分布的。处于中心位置的训练样本比四周的训练样本更加稀疏。
假设有一个二维特征空间,如上图所示的矩形,在矩形内部有一个内切的圆形。由于越接近圆心的样本越稀疏,因此,相比于圆形内的样本,那些位于矩形四角的样本更加难以分类。当维数变大时,特征超空间的容量不变,但单位圆的容量会趋于0,在高维空间中,大多数训练数据驻留在特征超空间的角落。散落在角落的数据要比处于中心的数据难于分类。
解决维度灾难问题:
主成分分析法PCA,线性判别法LDA
奇异值分解简化数据、拉普拉斯特征映射
Lassio缩减系数法、小波分析法等。
PCA可解决训练数据中存在数据特征过多或特征累赘的问题。核心思想是将m维特征映射到n维(n < m),这n维形成主元,是重构出来最能代表原始数据的正交特征。
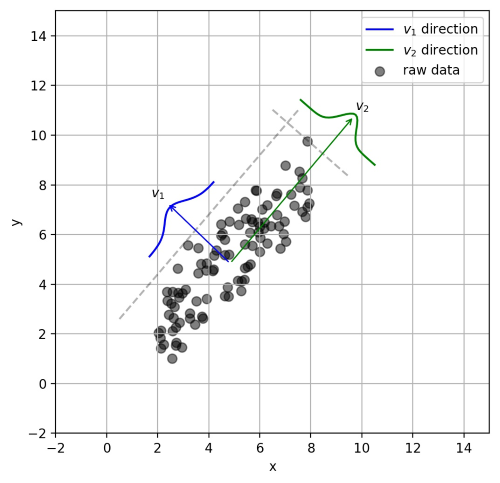
假设数据集是m个n维,(X(1),X(2)……..X(n)), 如果n=2,需要降维到n’=1,现在想找到某一维度方向代表这两个维度的数据。下图有u1, u2两个向量方向,但是哪个向量才是我们所想要的,可以更好代表原始数据集的呢?
从图可看出,u1,u2好,为什么呢?有以下两个主要评价指标:
如果我们需要降维的目标维数是其他任意维,则:
下面以基于最小投影距离为评价指标推理:
假设数据集是m个n维, (X(1),X(2)……..X(n)),且数据进行了中心化。经过投影变换得到新坐标为 {w_1,w_2,…,w_n},其中 w 是标准正交基,即 || w ||^2 = 1,w^T(i) w(j) = 0。
经过降维后,新坐标为 { w_1,w_2,…,w_n },其中 n’ 是降维后的目标维数。样本点 x^(i)在新坐标系下的投影为 z^(i) = (z^(i)1, z^(i)2, …, z^(i)n’ ),其中 z^(i)j = w^Tj x^(i)x^(i)$在低维坐标系里第 j 维的坐标。
如果用 $z^{(i)} $ 去恢复 $x^{(i)} $ ,则得到的恢复数据为
其中 W为标准正交基组成的矩阵。
考虑到整个样本集,样本点到这个超平面的距离足够近,目标变为最小化
对此式进行推理,可得:
在推导过程中,分别用x^(i) = Wz^(i), 矩阵转置公式 (AB)^T = B^T A^T,W^T W = I,z^(i) = W^T x^(i), 以及矩阵的迹,最后两步是将代数和转为矩阵形式。
由于W 的每一个向量 wj是标准正交基,
是数据集的协方差矩阵, 是一个常量。最小化
又可等价于
利用拉格朗日函数可得到:
对 W 求导,可得 , X X^T 是 n’ 个特征向量组成的矩阵,lambda为XX^T 的特征值。W 即为我们想要的矩阵。
对于原始数据,只需要 z^(i) = W^T X^(i) ,就可把原始数据集降维到最小投影距离的 n’$维数据集。
| 优缺点 | 简要说明 |
|---|---|
| 优点 | 1. 仅仅需要以方差衡量信息量,不受数据集以外的因素影响。 2.各主成分之间正交,可消除原始数据成分间的相互影响的因素。3. 计算方法简单,主要运算是特征值分解,易于实现。 |
| 缺点 | 1.主成分各个特征维度的含义具有一定的模糊性,不如原始样本特征的解释性强。2. 方差小的非主成分也可能含有对样本差异的重要信息,因降维丢弃可能对后续数据处理有影响。 |
降维的必要性:
降维的目的:
应用PCA算法前提是假设存在一个线性超平面,进而投影。那如果数据不是线性的, 就需要KPCA,数据集从 $n$ 维映射到线性可分的高维 N >n,然后再从 N维降维到一个低维度 n’(n’<n<N)$。
KPCA用到了核函数思想,使用了核函数的主成分分析一般称为核主成分分析(简称KPCA)。
假设高维空间数据由 n 维空间的数据通过映射产生。
$n$ 维空间的特征分解为:
其映射为:
通过在高维空间进行协方差矩阵的特征值分解,然后用和PCA一样的方法进行降维。由于KPCA需要核函数的运算,因此它的计算量要比PCA大很多。
| 异同点 | LDA | PCA |
|---|---|---|
| 相同点 | 1. 两者均可以对数据进行降维; 2. 两者在降维时均使用了矩阵特征分解的思想; 3. 两者都假设数据符合高斯分布; |
|
| 不同点 | 有监督的降维方法; | 无监督的降维方法; |
| 降维最多降到k-1维; | 降维多少没有限制; | |
| 可以用于降维,还可以用于分类; | 只用于降维; | |
| 选择分类性能最好的投影方向; | 选择样本点投影具有最大方差的方向; | |
| 更明确,更能反映样本间差异; | 目的较为模糊; |
线性判别分析LDA, 是一种经典的降维方法。和主成分分析PCA不考虑样本类别输出的无监督降维技术不同,LDA是一种监督学习的降维技术,数据集的每个样本有类别输出。
LDA分类思想简单总结如下:
左图思路:让不同类别的平均点距离最远的投影方式。
右图思路:让同类别的数据挨得最近的投影方式。
从上图直观看出,右图红色数据和蓝色数据在各自的区域来说相对集中,根据数据分布直方图也可看出,所以右图的投影效果好于左图,左图中间直方图部分有明显交集。
以上例子是基于数据是二维的,分类后的投影是一条直线。如果原始数据是多维的,则投影后的分类面是一低维的超平面。
输入:数据集 D={(x1,y1),(x2,y2)……..(xm,ym)},其中样本xi 是n维向量,yi属于{0,1},降维后的目标维度 d。定义:
Uj为一类数据的中心点,假设投影直线是向量 w,对任意样本xi,它在直线 w上的投影为 w^t xi,两个类别的中心点 u0 , u1在直线 w 的投影分别为 w^tu0 、w^t u1。
定义内散度矩阵:
定义类间散度矩阵:
所以设定优化的目标为:
根据广义瑞利商的性质,矩阵Sw^-1Sb 的最大特征值为 J(w) 的最大值,矩阵Sw^-1Sb 的最大特征值对应的特征向量即为 w。
LDA算法降维流程如下:
步骤:
###
逻辑回归可用于以下几个方面:
(1)用于概率预测。用于可能性预测时,得到的结果有可比性。比如根据模型进而预测在不同的自变量情况下,发生某病或某种情况的概率有多大。
(2)用于分类。实际上跟预测有些类似,也是根据模型,判断某人属于某病或属于某种情况的概率有多大,也就是看一下这个人有多大的可能性是属于某病。进行分类时,仅需要设定一个阈值即可,可能性高于阈值是一类,低于阈值是另一类。
(3)寻找危险因素。寻找某一疾病的危险因素等。
(4)仅能用于线性问题。只有当目标和特征是线性关系时,才能用逻辑回归。在应用逻辑回归时注意两点:一是当知道模型是非线性时,不适用逻辑回归;二是当使用逻辑回归时,应注意选择和目标为线性关系的特征。
(5)各特征之间不需要满足条件独立假设,但各个特征的贡献独立计算。
逻辑回归与朴素贝叶斯区别有以下几个方面:
(1)逻辑回归是判别模型, 朴素贝叶斯是生成模型,所以生成和判别的所有区别它们都有。
(2)朴素贝叶斯属于贝叶斯,逻辑回归是最大似然,两种概率哲学间的区别。
(3)朴素贝叶斯需要条件独立假设。
(4)逻辑回归需要求特征参数间是线性的。
线性回归与逻辑回归的区别如下描述:
(1)线性回归的样本的输出,都是连续值,而逻辑回归中只能取0和1。
(2)对于拟合函数也有本质上的差别:
线性回归:
逻辑回归:
其中,
可以看出,线性回归的拟合函数,是对f(x)的输出变量y的拟合,而逻辑回归的拟合函数是对为1类样本的概率的拟合。
那么,为什么要以1类样本的概率进行拟合呢,为什么可以这样拟合呢?
这个时候就能看出区别,在线性回归中:$\theta ^{T}x$为预测值的拟合函数;而在逻辑回归中为决策边界。下表2-3为线性回归和逻辑回归的区别。
表2-3 线性回归和逻辑回归的区别
| 线性回归 | 逻辑回归 | |
|---|---|---|
| 目的 | 预测 | 分类 |
| y^(i) | 未知 | (0,1) |
| 函数 | 拟合函数 | 预测函数 |
| 参数计算方式 | 最小二乘法 | 极大似然估计 |
下面具体解释一下:
拟合函数和预测函数什么关系呢?简单来说就是将拟合函数做了一个逻辑函数的转换,转换后使得
分类算法和回归算法是对真实世界不同建模的方法。分类模型是认为模型的输出是离散的,例如大自然的生物被划分为不同的种类,是离散的。回归模型的输出是连续的,例如人的身高变化过程是一个连续过程,而不是离散的。
因此,在实际建模过程时,采用分类模型还是回归模型,取决于你对任务(真实世界)的分析和理解。
接下来我们介绍常用分类算法的优缺点,如表2-1所示。
表2-1 常用分类算法的优缺点
| 算法 | 优点 | 缺点 |
|---|---|---|
| Bayes 贝叶斯分类法 | 1)所需估计的参数少,对于缺失数据不敏感。 2)有着坚实的数学基础,以及稳定的分类效率。 |
1)需要假设属性之间相互独立,这往往并不成立。(喜欢吃番茄、鸡蛋,却不喜欢吃番茄炒蛋)。 2)需要知道先验概率。 3)分类决策存在错误率。 |
| Decision Tree决策树 | 1)不需要任何领域知识或参数假设。 2)适合高维数据。 3)简单易于理解。 4)短时间内处理大量数据,得到可行且效果较好的结果。 5)能够同时处理数据型和常规性属性。 |
1)对于各类别样本数量不一致数据,信息增益偏向于那些具有更多数值的特征。 2)易于过拟合。 3)忽略属性之间的相关性。 4)不支持在线学习。 |
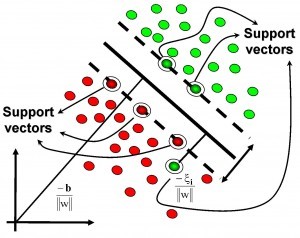
| SVM支持向量机 | 1)可以解决小样本下机器学习的问题。 2)提高泛化性能。 3)可以解决高维、非线性问题。超高维文本分类仍受欢迎。 4)避免神经网络结构选择和局部极小的问题。 |
1)对缺失数据敏感。 2)内存消耗大,难以解释。 3)运行和调参略烦人。 |
| KNN K近邻 | 1)思想简单,理论成熟,既可以用来做分类也可以用来做回归; 2)可用于非线性分类; 3)训练时间复杂度为O(n); 4)准确度高,对数据没有假设,对outlier不敏感; |
1)计算量太大。 2)对于样本分类不均衡的问题,会产生误判。 3)需要大量的内存。 4)输出的可解释性不强。 |
| Logistic Regression逻辑回归 | 1)速度快。 2)简单易于理解,直接看到各个特征的权重。 3)能容易地更新模型吸收新的数据。 4)如果想要一个概率框架,动态调整分类阀值。 |
特征处理复杂。需要归一化和较多的特征工程。 |
| Neural Network 神经网络 | 1)分类准确率高。 2)并行处理能力强。 3)分布式存储和学习能力强。 4)鲁棒性较强,不易受噪声影响。 |
1)需要大量参数(网络拓扑、阀值、阈值)。 2)结果难以解释。 3)训练时间过长。 |
| Adaboosting | 1)adaboost是一种有很高精度的分类器。 2)可以使用各种方法构建子分类器,Adaboost算法提供的是框架。 3)当使用简单分类器时,计算出的结果是可以理解的。而且弱分类器构造极其简单。 4)简单,不用做特征筛选。 5)不用担心overfitting。 |
对outlier比较敏感 |
分类评估方法主要功能是用来评估分类算法的好坏,而评估一个分类器算法的好坏又包括许多项指标。了解各种评估方法,在实际应用中选择正确的评估方法是十分重要的。
几个常用术语
1) True positives(TP): 被正确地划分为正例的个数,即实际为正例且被分类器划分为正例的实例数;
2) False positives(FP): 被错误地划分为正例的个数,即实际为负例但被分类器划分为正例的实例数;
3) False negatives(FN):被错误地划分为负例的个数,即实际为正例但被分类器划分为负例的实例数;
4) True negatives(TN): 被正确地划分为负例的个数,即实际为负例且被分类器划分为负例的实数。
表2-2 四个术语的混淆矩阵
1)P=TP+FN表示实际为正例的样本个数。
2)True、False描述的是分类器是否判断正确。
3)Positive、Negative是分类器的分类结果,如果正例计为1、负例计为-1,即positive=1、negative=-1。用1表示True,-1表示False,那么实际的类标=TF*PN,TF为true或false,PN为positive或negative。
4)例如True positives(TP)的实际类标=1*1=1为正例,False positives(FP)的实际类标=(-1)*1=-1为负例,False negatives(FN)的实际类标=(-1)*(-1)=1为正例,True negatives(TN)的实际类标=1*(-1)=-1为负例。
评价指标
1) 正确率(accuracy)
正确率是我们最常见的评价指标,accuracy = (TP+TN)/(P+N),正确率是被分对的样本数在所有样本数中的占比,通常来说,正确率越高,分类器越好。
2) 错误率(error rate)
错误率则与正确率相反,描述被分类器错分的比例,error rate = (FP+FN)/(P+N),对某一个实例来说,分对与分错是互斥事件,所以accuracy =1 - error rate。
3) 灵敏度(sensitivity)
sensitivity = TP/P,表示的是所有正例中被分对的比例,衡量了分类器对正例的识别能力。
4) 特异性(specificity)
specificity = TN/N,表示的是所有负例中被分对的比例,衡量了分类器对负例的识别能力。
5) 精度(precision)
precision=TP/(TP+FP),精度是精确性的度量,表示被分为正例的示例中实际为正例的比例。
6) 召回率(recall)
召回率是覆盖面的度量,度量有多个正例被分为正例,recall=TP/(TP+FN)=TP/P=sensitivity,可以看到召回率与灵敏度是一样的。
7) 其他评价指标
计算速度:分类器训练和预测需要的时间;
鲁棒性:处理缺失值和异常值的能力;
可扩展性:处理大数据集的能力;
可解释性:分类器的预测标准的可理解性,像决策树产生的规则就是很容易理解的,而神经网络的一堆参数就不好理解,我们只好把它看成一个黑盒子。
8) 精度和召回率反映了分类器分类性能的两个方面。如果综合考虑查准率与查全率,可以得到新的评价指标F1-score,也称为综合分类率:$F1=\frac{2 \times precision \times recall}{precision + recall}$。
1 | 为了综合多个类别的分类情况,评测系统整体性能,经常采用的还有微平均F1(micro-averaging)和宏平均F1(macro-averaging )两种指标。 |
ROC曲线和PR曲线
如图2-3,ROC曲线是(Receiver Operating Characteristic Curve,受试者工作特征曲线)的简称,是以灵敏度(真阳性率)为纵坐标,以1减去特异性(假阳性率)为横坐标绘制的性能评价曲线。可以将不同模型对同一数据集的ROC曲线绘制在同一笛卡尔坐标系中,ROC曲线越靠近左上角,说明其对应模型越可靠。也可以通过ROC曲线下面的面积(Area Under Curve, AUC)来评价模型,AUC越大,模型越可靠。
图2-3 ROC曲线
PR曲线是Precision Recall Curve的简称,描述的是precision和recall之间的关系,以recall为横坐标,precision为纵坐标绘制的曲线。该曲线的所对应的面积AUC实际上是目标检测中常用的评价指标平均精度(Average Precision, AP)。AP越高,说明模型性能越好。
根据数据类型的不同,对一个问题的建模有不同的方式。依据不同的学习方式和输入数据,机器学习主要分为以下四种学习方式。
特点:监督学习是使用已知正确答案的示例来训练网络。已知数据和其一一对应的标签,训练一个预测模型,将输入数据映射到标签的过程。
常见应用场景:监督式学习的常见应用场景如分类问题和回归问题。
算法举例:常见的有监督机器学习算法包括支持向量机(Support Vector Machine, SVM),朴素贝叶斯(Naive Bayes),逻辑回归(Logistic Regression),K近邻(K-Nearest Neighborhood, KNN),决策树(Decision Tree),随机森林(Random Forest),AdaBoost以及线性判别分析(Linear Discriminant Analysis, LDA)等。深度学习(Deep Learning)也是大多数以监督学习的方式呈现。
定义:在非监督式学习中,数据并不被特别标识,适用于你具有数据集但无标签的情况。学习模型是为了推断出数据的一些内在结构。
常见应用场景:常见的应用场景包括关联规则的学习以及聚类等。
算法举例:常见算法包括Apriori算法以及k-Means算法。
特点:在此学习方式下,输入数据部分被标记,部分没有被标记,这种学习模型可以用来进行预测。
常见应用场景:应用场景包括分类和回归,算法包括一些对常用监督式学习算法的延伸,通过对已标记数据建模,在此基础上,对未标记数据进行预测。
算法举例:常见算法如图论推理算法(Graph Inference)或者拉普拉斯支持向量机(Laplacian SVM)等。
特点:弱监督学习可以看做是有多个标记的数据集合,次集合可以是空集,单个元素,或包含多种情况(没有标记,有一个标记,和有多个标记)的多个元素。 数据集的标签是不可靠的,这里的不可靠可以是标记不正确,多种标记,标记不充分,局部标记等。已知数据和其一一对应的弱标签,训练一个智能算法,将输入数据映射到一组更强的标签的过程。标签的强弱指的是标签蕴含的信息量的多少,比如相对于分割的标签来说,分类的标签就是弱标签。
算法举例:举例,给出一张包含气球的图片,需要得出气球在图片中的位置及气球和背景的分割线,这就是已知弱标签学习强标签的问题。
在企业数据应用的场景下, 人们最常用的可能就是监督式学习和非监督式学习的模型。 在图像识别等领域,由于存在大量的非标识的数据和少量的可标识数据, 目前半监督式学习是一个很热的话题。
监督学习是使用已知正确答案的示例来训练网络,每组训练数据有一个明确的标识或结果。想象一下,我们可以训练一个网络,让其从照片库中(其中包含气球的照片)识别出气球的照片。以下就是我们在这个假设场景中所要采取的步骤。
步骤1:数据集的创建和分类
首先,浏览你的照片(数据集),确定所有包含气球的照片,并对其进行标注。然后,将所有照片分为训练集和验证集。目标就是在深度网络中找一函数,这个函数输入是任意一张照片,当照片中包含气球时,输出1,否则输出0。
步骤2:数据增强(Data Augmentation)
当原始数据搜集和标注完毕,一般搜集的数据并不一定包含目标在各种扰动下的信息。数据的好坏对于机器学习模型的预测能力至关重要,因此一般会进行数据增强。对于图像数据来说,数据增强一般包括,图像旋转,平移,颜色变换,裁剪,仿射变换等。
步骤3:特征工程(Feature Engineering)
一般来讲,特征工程包含特征提取和特征选择。常见的手工特征(Hand-Crafted Feature)有尺度不变特征变换(Scale-Invariant Feature Transform, SIFT),方向梯度直方图(Histogram of Oriented Gradient, HOG)等。由于手工特征是启发式的,其算法设计背后的出发点不同,将这些特征组合在一起的时候有可能会产生冲突,如何将组合特征的效能发挥出来,使原始数据在特征空间中的判别性最大化,就需要用到特征选择的方法。在深度学习方法大获成功之后,人们很大一部分不再关注特征工程本身。因为,最常用到的卷积神经网络(Convolutional Neural Networks, CNNs)本身就是一种特征提取和选择的引擎。研究者提出的不同的网络结构、正则化、归一化方法实际上就是深度学习背景下的特征工程。
步骤4:构建预测模型和损失
将原始数据映射到特征空间之后,也就意味着我们得到了比较合理的输入。下一步就是构建合适的预测模型得到对应输入的输出。而如何保证模型的输出和输入标签的一致性,就需要构建模型预测和标签之间的损失函数,常见的损失函数(Loss Function)有交叉熵、均方差等。通过优化方法不断迭代,使模型从最初的初始化状态一步步变化为有预测能力的模型的过程,实际上就是学习的过程。
步骤5:训练
选择合适的模型和超参数进行初始化,其中超参数比如支持向量机中核函数、误差项惩罚权重等。当模型初始化参数设定好后,将制作好的特征数据输入到模型,通过合适的优化方法不断缩小输出与标签之间的差距,当迭代过程到了截止条件,就可以得到训练好的模型。优化方法最常见的就是梯度下降法及其变种,使用梯度下降法的前提是优化目标函数对于模型是可导的。
步骤6:验证和模型选择
训练完训练集图片后,需要进行模型测试。利用验证集来验证模型是否可以准确地挑选出含有气球在内的照片。
在此过程中,通常会通过调整和模型相关的各种事物(超参数)来重复步骤2和3,诸如里面有多少个节点,有多少层,使用怎样的激活函数和损失函数,如何在反向传播阶段积极有效地训练权值等等。
步骤7:测试及应用
当有了一个准确的模型,就可以将该模型部署到你的应用程序中。你可以将预测功能发布为API(Application Programming Interface, 应用程序编程接口)调用,并且你可以从软件中调用该API,从而进行推理并给出相应的结果。
最大期望算法(Expectation-Maximization algorithm, EM),是一类通过迭代进行极大似然估计的优化算法,通常作为牛顿迭代法的替代,用于对包含隐变量或缺失数据的概率模型进行参数估计。
最大期望算法基本思想是经过两个步骤交替进行计算:
第一步是计算期望(E),利用对隐藏变量的现有估计值,计算其最大似然估计值;
第二步是最大化(M),最大化在E步上求得的最大似然值来计算参数的值。
M步上找到的参数估计值被用于下一个E步计算中,这个过程不断交替进行。
对于m个样本观察数据x=(x^{1},x^{2},…,x^{m}),现在想找出样本的模型参数\thet
a,其极大化模型分布的对数似然函数为:
如果得到的观察数据有未观察到的隐含数据z=(z^{(1)},z^{(2)},…z^{(m)}),极大化模型分布的对数似然函数则为:
由于上式不能直接求出\theta,采用缩放技巧:
上式用到了Jensen不等式:
并且引入了一个未知的新分布Q_i(z^{(i)})。
此时,如果需要满足Jensen不等式中的等号,所以有:
由于Q_i(z^{(i)})是一个分布,所以满足
综上,可得:
如果Q_i(z^{(i)}) = P( z^{(i)}|x^{(i)};\theta),则第(1)式是我们的包含隐藏数据的对数似然的一个下界。如果我们能极大化这个下界,则也在尝试极大化我们的对数似然。即我们需要最大化下式:
简化得:
以上即为EM算法的M步,\sum\limits_{z^{(i)}}Q_i(z^{(i)})log{P(x^{(i)}, z^{(i)};\theta)}可理解为logP(x^{(i)}, z^{(i)};\theta) 基于条件概率分布Q_i(z^{(i)}) 的期望。以上即为EM算法中E步和M步的具体数学含义。
考虑上一节中的(a)式,表达式中存在隐变量,直接找到参数估计比较困难,通过EM算法迭代求解下界的最大值到收敛为止。
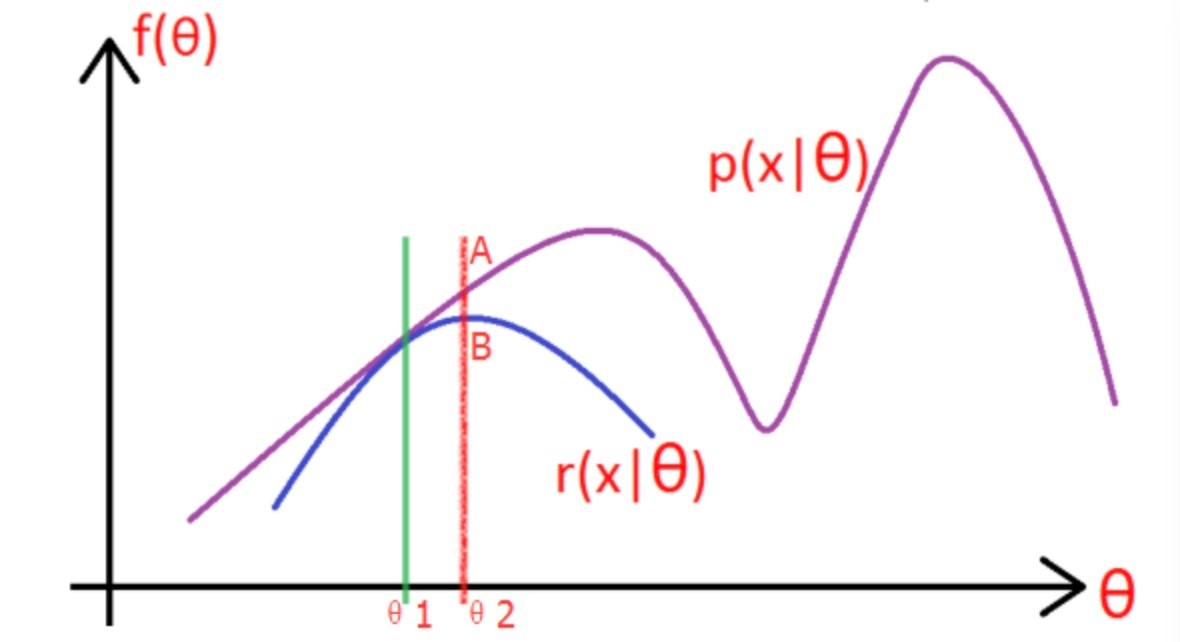
图片中的紫色部分是我们的目标模型p(x|\theta),该模型复杂,难以求解析解,为了消除隐变量z^{(i)}的影响,我们可以选择一个不包含$z^{(i)}$的模型r(x|\theta),使其满足条件r(x|\theta) \leqslant p(x|\theta) 。
求解步骤如下:
(1)选取\theta_1,使得r(x|\theta_1) = p(x|\theta_1),然后对此时的r求取最大值,得到极值点\theta_2,实现参数的更新。
(2)重复以上过程到收敛为止,在更新过程中始终满足r \leqslant p .
输入:观察数据x=(x^{(1)},x^{(2)},…x^{(m)}),联合分布p(x,z ;\theta),条件分布p(z|x; \theta),最大迭代次数J
1)随机初始化模型参数\theta的初值\theta^0。
2)for j from 1 to j:
a) E步。计算联合分布的条件概率期望:
b) M步。极大化$L(\theta, \theta^{j})$,得到\theta^{j+1}$\:
c) 如果\theta^{j+1}收敛,则算法结束。否则继续回到步骤a)进行E步迭代。
输出:模型参数\theta。
双目立体视觉是基于视差原理,从双目相机中获取的多幅图像中恢复被测物体三维几何信息的方法。如图,对于空间物体表面任意一点,如果从左右2个摄像机同时观察P,并能确定在左摄像机图像上的点Pl与右摄像机图像上的点Pr是空间同一点P的图像点(称Pl与Pr,为共轭对应点),则可计算出空间点P的三维坐标(包含距离信息)。基于双目立体视觉的测距系统包含摄像机标定、立体校正、立体匹配和三维重建等步骤。
根据三角形相似原理:
z/f=(x-b)/xr=x/xl=y/yl
解方程得:
z=bf/d, x=zxl/d, y=z*y/f
由此可知:想要得到距离z,必须知道:
1、相机焦距f,左右相机基线b(可以通过先验信息或者相机标定得到)。
2、视差 :d=xl-xr,即左相机像素点(xl, yl)和右相机中对应点(xr, yr)的关系,这是双目视觉的核心问题。
对于左图中的一个像素点,来确定该点在右图中的位置,不需要在整个图像中地毯式搜索,需要用到极线约束。如上图所示。O1,O2是两个相机,P是空间中的一个点,P和两个相机中心点O1、O2形成了三维空间中的一个平面PO1O2,称为极平面(Epipolar plane)。极平面和两幅图像相交于两条直线,这两条直线称为极线(Epipolar line)。P在相机O1中的成像点是P1,在相机O2中的成像点是P2,但是P的位置是未知的。我们的目标是:对于左图的P1点,寻找它在右图中的对应点P2,这样就能确定P点的空间位置。极线约束(Epipolar Constraint)是指当空间点在两幅图像上分别成像时,已知左图投影点p1,那么对应右图投影点p2一定在相对于p1的极线上,这样可以极大的缩小匹配范围。即P2一定在对应极线上,所以只需要沿着极线搜索便可以找到P1的对应点P2。
当两个相机光心不是处于同一水平面时:这种情况下拍摄的两张左右图片,右图中对应的极线是右图中的多条直线,也就是对应的搜索区域。这多条直线并不是水平的,如果进行逐点搜索效率非常低。
(3)图像矫正技术:
像矫正是通过分别对两张图片用单应性矩阵变换得到,目的是把两个不同方向的图像平面(下图中灰色平面)重新投影到同一个平面且光轴互相平行(下图中黄色平面),这样转化为理想情况的模型。
经过图像矫正后,左图中的像素点只需要沿着水平的极线方向搜索对应点,从下图中我们可以看到三个点对应的视差(红色双箭头线段)是不同的,越远的物体视差越小,越近的物体视差越大。
1 | #使用普通摄像头进行深度估计 |
运行结果: